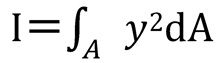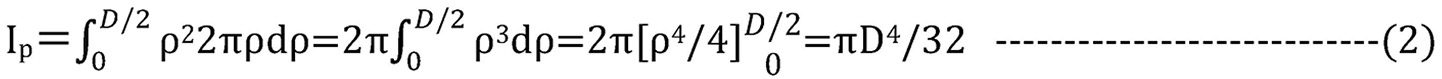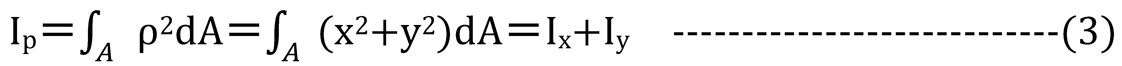博士「おーい、あるる、3時のおやつの時間じゃぞ〜♪」

あるる「はーい！　今いきまーす。・・・あっ！　今日はおせんべいシリーズですね」

博士「いろんな種類があるから、好きなのをお食べ」

あるる「わーい、いっただきまーす。あっ、ひねり揚げだ！　これ、おじいちゃんの大好物なんですよねー」

博士「わしも大好きじゃ。どうやら好みが似ているようじゃのう。ふぉっふぉっふぉっ」

あるる「・・・（パリパリ）」

博士「おや、あるるよ。さっき「ひねり揚げ」と言ったか？」

あるる「・・・（ポリポリ）・・・はい、言いましたけど、なにか？（パリパリ）」

博士「わしはずっと“ねじり揚げ”と呼んでおるが・・・」

あるる「どっちも同じじゃないですか。美味しいことには間違いなし！ですから」

博士「ふむ。いつみても、この美しいねじり・・・やっぱり“ねじり揚げ”と呼びたいぞ」

あるる「はいはい。じゃ、そうしましょう。ねじり、ねじり揚げです（ポリポリ）」

博士「よし。（パリパリ）やっぱりねじり揚げは美味しいのぅ♪」

あるる「（ホント、どっちでもいいのに笑）←あるる心の声」

博士「はっ！そうじゃ！　わしとしたことが！　あるるにまだ、大事なことを伝えておらんかった！」

あるる「なんですか、急に」

博士「ねじり剛性に関わる係数についてじゃ！」

あるる「え？？　なんて？」

博士「断面二次極モーメントじゃ！」

あるる「えー、またモーメント?!　わかりました。教えてください。でも、テストはしませんよね、ね？」

断面二次モーメントと似たもので、断面二次極モーメントと言うものがあります。

断面二次モーメントは、曲げ剛性に関わる係数でしたが、断面二次極モーメントはねじり剛性に関わる係数です。

【今月のまめ知識　第9回】「ねじり剛性」についてに出てきましたが、今回はこの断面二次極モーメントについて説明します。

第86回の断面二次モーメントの正体、第87回の断面係数で説明した通り、断面二次モーメントは微小領域までの距離の二乗に微小面積を乗じたものを断面全体で積分した以下の式で表されます。

これと同じ考え方で円形断面を考えると

となり、このIpが断面二次極モーメントです。

Fig.2

では、円形断面の断面二次極モーメントを求めてみると

微小面積dAは半径ρで幅がdρの円環なので、2πρdρとなり、これをρで積分すればよいので以下となります。

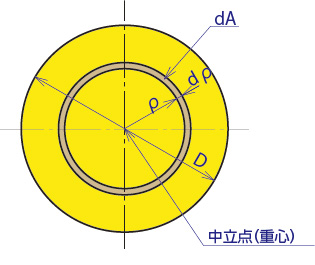
断面二次極モーメントの単位はmm⁴で、軸の直径の4乗に比例します。

断面二次モーメントではひずみの発生しないところを中立軸と呼びましたが、

同じようにねじれひずみが生じない点を中立点と呼び、それは断面の重心になります。

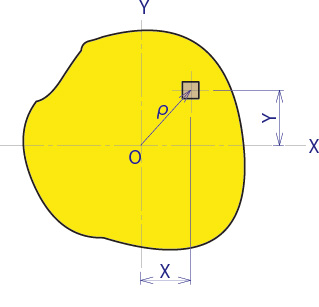
下図のような、円形ではない場合

Fig.2

断面二次極モーメントは

ρ²＝x²+y²であり、式(1)より

となり、平面図形の任意の点Oに関する断面二次極モーメントは、この点を通る二つの互いに垂直な軸x及びyに関する断面二次モーメントの和に等しくなります。

但し、これは単純な形状においてのみ成り立ち、外周にナット挿入溝を持つ構造用アルミフレームにおいては成り立ちません。

（当社では別の方法でIpの値を定義していますので必要な場合はお問い合わせください）

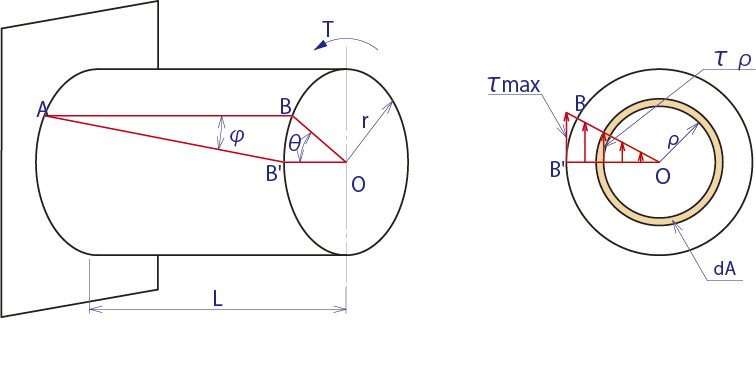
次に、ねじりモーメントとねじり応力、断面二次極モーメントの関係について下図で説明します。

Fig.3

φ：せん断角

θ：ねじれ角

T：ねじりモーメント

G：横弾性係数

tanφが、せん断ひずみγとなる

材料の弾性限度内でせん断ひずみγは、せん断応力τに比例するので

ねじりによって生じるせん断応力、ねじり応力τは

中心からある半径ρの位置の微小面積dAに生じているねじり応力τρは

dAの面積におきている全応力は、τρdAとなるので中心Oに関するモーメントをdRとすれば

このモーメントを断面全体に取った全モーメントRは

RはねじりモーメントTに抵抗して生じるモーメントで向きが反対で大きさは等しくなる。
よって式(1)、(9)より

という形で、ねじりモーメントとねじり応力、断面二次極モーメントの関係が導かれます。

博士「どうじゃ、あるる、断面二次極モーメントについて、理解できたかの？」

あるる「う〜ん・・・とっても難しかったですが、面白かったです！　おうちに帰って復習すれば、ちゃんと頭に入るような気がしています」

博士「おお、えらいぞ、あるる。そうやって自ら「わかろう」と思う気持ちが大切なんじゃ！」

あるる「はいっ！　頑張ります！　そしてこれからは、ひねり揚げのことを「ねじり揚げ」と呼びます！」

博士「もしや、一番気になっていたのはそこだったのでは・・・？　ふぉっふぉっふぉっ、あるるらしいのぅ。まだ残っているから、持って帰っておじいちゃんと一緒にお食べ」

あるる「わーい、ありがとうございます！＼(^o^)／！　ねじり万歳！！！」