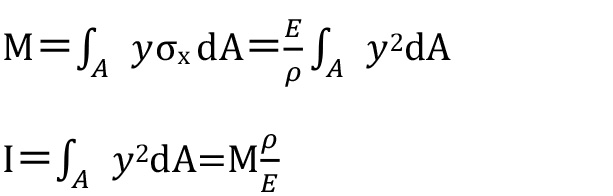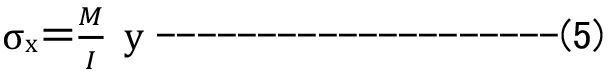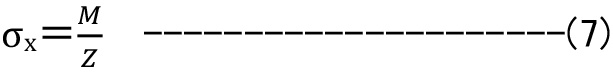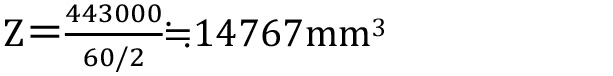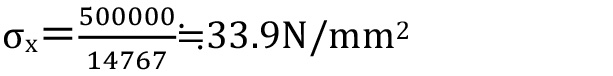博士「おはよう、あるる。この暑い中、花壇の掃除とは感心じゃのう〜」

あるる「あ、博士、おはようございます！　紫陽花がこんなに綺麗に咲いてくれたので、もっと綺麗にしてあげようと思って♪」

博士「うんうん、えらいのぅ。よし、わしも手伝おう」

あるる「ありがとうございます！　雑草、思った以上にたくさん生えているので、助かります」

博士「土いじりは久しぶりじゃから、なかなか楽しいのぅ」

あるる「あっ！　こんな長い枝が！」

博士「おお、元気がよかったんじゃのう。でも、そのままではゴミ袋を突き破ってしまうから、短くしておくれ」

あるる「そうですね。えい、えいえいーーー！（汗）」

あるる「あれ？　折れない・・・どころか全然曲がりませーん」

博士「おお、そうか。見た目より断面係数が高いのじゃのう。根性があってよろしい（笑）」

あるる「えっ？　何が高いって？　だんめん・・・けいす・・う？」

博士「そうじゃ、断面係数じゃ。『二次モーメント』についてはこの前説明したじゃろう。それととっても関連性があるものじゃ」

あるる「あ、に、二次モーメント・・・ですか（そわそわ）」

博士「どうした、あるる、急ににそわそわして。まさか覚えてないわけではあるまい。そもそも二次モーメントとは・・・」

あるる「あ、あ、博士、ジャスト・モーメント・プリーズ！　講義はお掃除の後でお願いします！　忘れてません！　難しかったからソワソワしただけですから！」

前回は、断面二次モーメントについて説明しました。

今回は引き続き断面二次モーメントと関連性のある「断面係数」について説明します。

断面係数は断面二次モーメントと同様に、断面形状からその材料の強さを表すものです。

断面二次モーメントは、たわみ量を算出するときに、断面係数は応力度を算出するときに使います。

言い換えると曲げモーメントに対して

断面二次モーメントはどれだけ曲がりにくいか

断面係数はどれだけ耐えれるか

を表す数値ですが、両方とも材質には関係ありません。

断面形状の性能を表すものです。

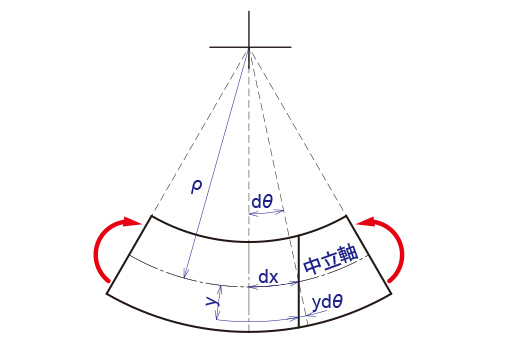
断面二次モーメントは、曲がりにくさ、つまり曲げモーメントが掛かったときに発生する曲率半径との関係を導くことが出来、ここからたわみ量も求まるわけです。

次式は前回説明していないので、以下の補足を参照してください。

**************************************************************************

補足：式(1)については、前回省略したので、以下にて説明。

梁の中のひずみεxは、中立軸上の微小距離dxの両端の面の交点が曲率中心であり、面同士の角度θとの関係から距離yの位置で以下の式となります。

そして【今月のまめ知識　第55回】弾性係数と剛性で説明したように、軸方向の応力σ_xは縦弾性係数との関係より

前回の式(1)より dM＝y・σ_x・dA　これに上記(3)を代入して積分すると

となり、ここから今回の式(1)が導かれます。

*****************************************************************************

式(1)を書き換え

補足説明の式(3)に(4)を代入して

この式でIとyの関係で定義されるのが、断面係数Zです。

ここで、yは曲げ応力が最大となる、中立軸から最も離れた位置までの距離です。

式(5)(6)より

となります。

このσ_xが曲げ応力ですが、曲げモーメント(M)を断面係数(Z)で除した値であり、

断面係数(Z)は断面二次モーメント(I)を距離(y)で除した値です。

つまり、断面二次モーメントと同じく、材質には全く関係のない値です。

実用的には曲げモーメントから断面係数を使って曲げ応力を求めて、使用する材料の許容応力から安全率を検討するわけです。

式(6)のyは上下対象の断面においては中立軸が高さ寸法(h)の中点にあるので

となります。

上下対象の例としてAFS-6060-6の断面係数(Z)と、曲げモーメント500Nmが掛かった場合の
曲げ応力(σ_x)を求めてみましょう。

AFS-6060-6は、Ix=443000mm⁴、h＝60mmなので

ここで500Nmの曲げモーメントが掛かったならば、その応力は

となります。

これは最上面、最下面で方向が逆で同じ値となります。

しかし、上下非対称の場合には、中立軸は高さの中点ではありません。

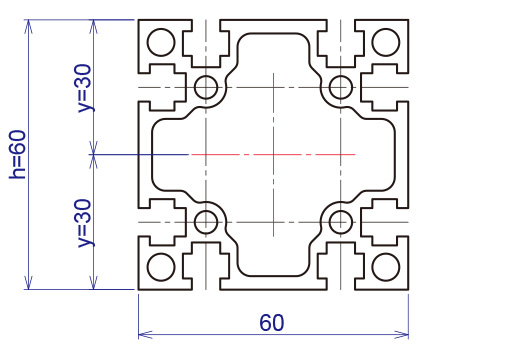
この例としてAFS-606015-6の断面係数(Z)と、曲げモーメント500Nmが掛かった場合の曲げ応力(σ_x)を求めてみましょう。

AFS-606015-6は、Ix＝240000mm⁴、y₁＝21.2mm、y₂＝38.8mmなので

500Nmの曲げモーメントが掛かったならば

となり、最上面には最下面の2倍近い応力が掛かることになります。

このように、上下非対称の断面においては中立軸から離れている側の面での曲げ応力に注意が必要です。

梁の検討をする場合には、たわみ量とともに曲げ応力を求め、その安全率を検討する必要があります。