博士「よ〜し、午後の授業を始めるぞ〜」

あるる「はぁ〜い！」

博士「おお、元気がよいのぅ。さてはお弁当が美味しかったと見える」

あるる「はいっ！今日は大好物のエビフライが入ってましたから！！（ガッツポーズ）」

博士「それはよかったのぅ。今日の授業はちと難解じゃが、その元気があればきっと乗り切れるぞ」

あるる「え？　難解・・・？」

博士「そうじゃ。今日のテーマは『モーメント』じゃ。まずは一次から行くぞ〜。まずは断面・・・」

あるる「え？え？ (^◇^;) そんなにいきなり・・・ちょ、ちょっと待ってくださいよ〜っ！！」

博士「（ニヤリ）なに？　待てとな？（ニヤリ）それを英語で言えたら、待ってしんぜよう（ニヤリ）」

あるる「へ？　英語？　今日はやけにハードルが高いなぁ〜・・・えっと、えっと・・・はっ！

ジャストモーメント、プリ〜ズ！！」

博士「ふぉっふぉっふぉっふぉっ（大笑）　よくできました！！　さすがあるるじゃ」

あるる「もう〜、博士ったら〜、『モーメント』って言わせたかっただけでしょ〜（ぷんぷん）」

剛性を語るうえで、必ず登場するのが断面二次モーメントです。

日常的に良く使用する値ですが、この意味は材料力学の本では難解な式が多くちょっとわかりにくいのではと思い、今回は計算式は最小限として説明してみたいと思います。

二次と言うくらいですから、一次があります。

まず断面一次モーメントからです。

一次も二次も、名前のややこしさが理解を難しくしているように思います。

力のモーメントと言うのは「力 × 距離」です。

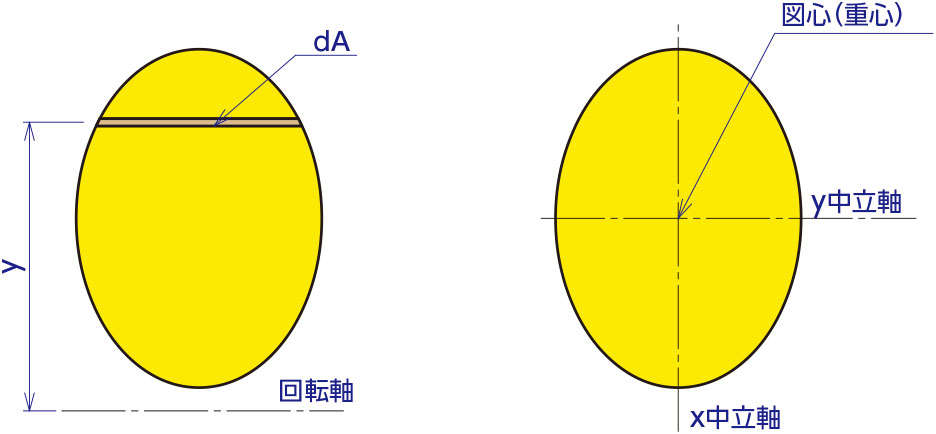
図の物体に均等に応力σが働いているとしたときに微小面積dAに応力を掛ければ力になり、これに回転軸からの距離yを掛ければこの部分についての微小モーメントdMとなります。

dM＝y・σ・dA　------------（１）

ここで両方の項からσの成分を除外して全面積で積分したものが断面一次モーメント[G]です。

G＝∫y・dA　------------（2）

ですから考え方の元は、「力 × 距離」になっていたわけなので、考え方とすればモーメントですね。面積を力とみなしてそれに距離を掛け算しているので、単位は、［m³］となります。

Fig.1

そしてこの回転軸を図形の中心に持っていくと、yにプラスとマイナスが出来るので、積分した結果である断面一次モーメントはゼロになります。この位置が中立軸です。

そして、X方向とY方向の中立軸の交点が図心（重心）です。

理論的にはこの図形の形状を均一な厚さの薄板として、図心を針の上に載せればバランスが取れるわけです。つまり自分の質量が荷重であり、図心位置に対するこの荷重のモーメントの総和がゼロという事になります。

ちょっと考えてもらうとわかりますが、物の重心を求める時に質量と座標を掛け算して総和を求める手法と同じであり、要は断面一次モーメントとは図心（重心）を求めるためのものです。

次に断面二次モーメントです。

部材の曲げ剛性は断面積だけではなく、形状によって決まります。曲げ剛性が高いという事は曲げモーメントに対して反対向きの抵抗モーメントが大きければ良いわけです。

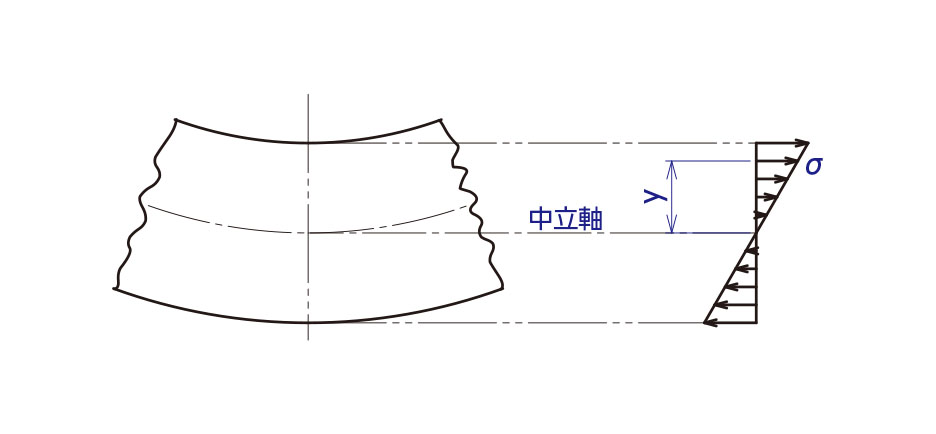
断面一次モーメントでは全面に渡って均一な応力としていましたが、曲げの場合、曲げモーメントに対して微小断面に生じる応力σは、フックの法則により中立軸からの距離yに比例します。

Fig.2

つまり、特定の微小面積に掛かる微小モーメントは、式（１）にもう一回yを乗じる必要があります。

dM＝y²・σ・dA　------------（3）

これを全面積で積分したものが断面二次モーメント[I]です。

I＝∫y²・dA　------------（4）

yの2乗となるので、必ず正の値となり、断面一次モーメントのように中立軸回りでもゼロとはなりません。微小面積dAに距離yを掛けた値が応力の代わりであり、それに距離yを掛け算していてyが2乗になるので二次という事になるわけです。

微小面積dAはx方向とy方向の積であるので、断面二次モーメントはy寸法の3乗に、x寸法の1乗に比例することになり、単位は[m⁴]となります。

●全面積で均一に応力が掛かった状態での微小モーメントの総和が断面一次モーメントであり、中立軸および図心（重心）を求めるためのもの。

●曲げモーメントによって生じる中立軸からの距離に比例した応力が掛かった状態での微小モーメントの総和が断面二次モーメントであり、寸法・形状による梁の曲げにくさを表す値である。

という事になります。

なお、断面二次モーメントは「慣性モーメント」とも言います。英語では「moment of inertia of area」となり、面積の慣性モーメントと言う表現になっています。

慣性モーメントと言うと回転体の回りにくさを表す値ですが、梁の曲げにくさとどういう関連があるのかというと

・動力学で言うところの慣性モーメントは、微小質量と距離を掛け算した値の総和であり、質量の慣性モーメントとなり、回転しにくさを表す。

・静力学で言うところの慣性モーメントは、微小面積と距離を掛け算した値の総和であり、面積の慣性モーメントとなり、変形しにくさを表す。

と、なります。

静力学では質量が無くなる、つまり形状だけなので厚さが無くなり面積となるわけです。

慣性モーメントの中で、静力学の場合において断面二次モーメントと言うと考えてよいのではと思います。

また、動力学で慣性モーメントの大きなフライホイールなどの断面形状と、静力学で断面二次モーメント（慣性モーメント）の大きなI型鋼などの断面形状が似ていることなどを見ると、次元を超えた共通性を見出せます。

博士「どうじゃな、あるる。わかったかの？　やけに静かじゃが・・・」

あるる「・・・・・」

博士「おやおや、固まってしまっておるぞ。おーい、あるるよ〜、戻ってまいれ〜」

あるる「（ハッッ！）　あ、博士、どうしたんですか？　まだ授業中ですよ、そんな大きな声を出して」

博士「あるるよ、もう授業は終わったのだぞ」

あるる「ええっ、いつのまに?!（驚）」

博士「本気で驚いておる。もしや難解すぎて、違う次元に旅立ってしまったていたのか？　ふぉっふぉっふぉっ。だとしたらある意味、最後まで私の話をちゃんと聞いていたことになるのぉ〜」

あるる「？？？？」