博士「あるるよ、以前勉強した「ヤング率」は覚えておるか？」

あるる「はい、もちろんです。ヤングさんが見つけたナウでヤングな「縦弾性係数」のことですよね?!」

博士「余計なモノがくっついているが・・・まぁ、そうじゃな、縦弾性係数のことじゃ」

あるる「それがどうしたんですか？　またヤングマンが歌いたくなったとか？」

博士「ゆうべ熱唱したから、当分は大丈夫じゃ」

あるる「歌ったんですね（笑）」

博士「あるるよ、今日は縦弾性係数をさらに深掘りして、「曲げ」の不思議に迫ってみるぞよ」

あるる「へっ？　“まげ”？　ナウでヤングな、ちょんまげ・・・？？？」

博士「お前の想像していることは大抵わかる。最初に言っておくが、そっちではないからな」

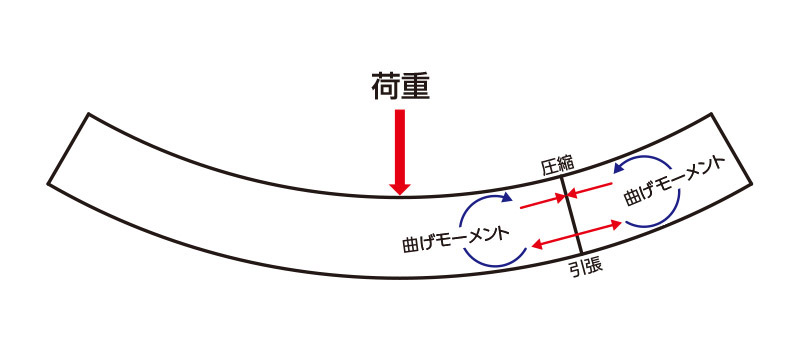
梁が曲がるという事は、曲率の内側が圧縮で外側が引張りという状態であるという事を

【第53回】縦弾性係数（ヤング率）にて説明しました。

ここで面白いことは、上下方向に荷重が作用しているのに、材料はそれを水平方向の応力に変換して受けているということです。

図のように、材料の中心より上側と下側では応力の方向が逆であり、偶力（大きさが等しく作用線が平行で互いに逆向きの力）となります。

偶力は物体を並進運動させることはありませんが、その中点にモーメントとして働きます。

梁に荷重を掛けると、梁を回転させようとする曲げモーメントと、せん断力がかかります。

そして、この曲げモーメントに対抗するために、梁は内部で圧縮と引張りという形で偶力モーメントを発生させて対抗するのです。

また、梁の高さが低いと偶力が小さい上に中点からの距離も短く、抵抗力としてのモーメントが非常に小さく弱い梁となります。

そして、もっとも破壊しやすい場所は、曲げモーメントが最大となるポイントです。

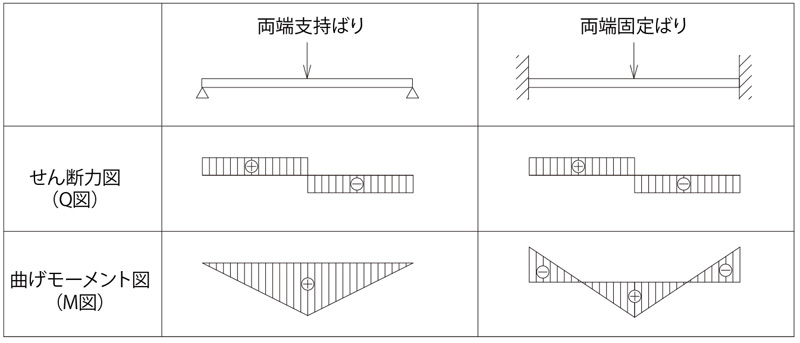
応力図

曲げモーメントが最大となる点の荷重側の面で圧縮応力が、荷重と反対面で引張り応力が最大となります。