とある平和なお昼時。

博士とあるる、二人揃って楽しい昼食の時間を迎えている。

「いっただきまーす♪♪♪」

 

あるる「あれ？なんで割れないんだ？　うんしょ。うんしょ」

 

 

 

前号でお話した「荷重」に続き、今回は「応力」についてお話しましょう。

 

応力とは

 

前号でもお話しましたが、部材にかかる「荷重」（Load）という外力に対し、

つり合うために物体内部に生じる単位面積当たりの内力を「応力」（Stress）と言います。

つり合うということは、外力は部材を変形させようとしますが、

それに対応して大きさが等しく、向きが反対の力を発生させるということです。

 

つり合わない場合は、変形が進行して破壊に至ったり、

部材そのものが移動したりするということになります。

 

応力について考える場合、下図のように仮想断面を考えるとわかります。

荷重がかかった時に棒がちぎれて左右に飛んでいかないためには、

荷重と等しく方向が逆の内力が存在しなければなりません。これが「応力」です。

 


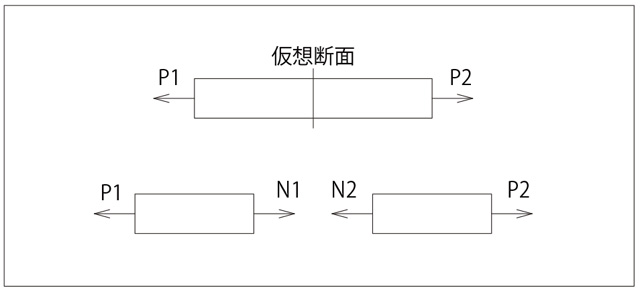
外力・内力

 

応力の種類

 

応力には以下の3種類があります。

 

１）軸方向力

部材の軸方向に作用し、部材を伸縮させようとする力です。

引張力を（＋）、圧縮力を（－）で表します。

 

２）せん断力

部材の軸直角方向に作用し、ずれの変形を生じさせようとする力です。

向きが逆の一対の力で、時計回りを（＋）、反時計回りを（－）で表します。

 

３）曲げモーメント

部材を曲げようとする力です。湾曲の外側には引張力、内側には圧縮力がかかります。

部材の下側が伸びる場合を（＋）、上側が伸びる場合を（－）で表します。

 


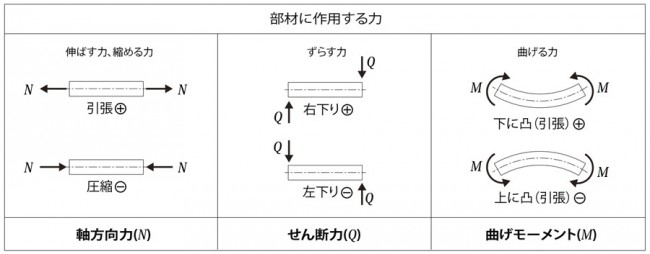
応力の種類

 

これらを表す、応力図というものがあります。

これを使うと部材にどのような応力がかかっているかがわかります。

参考に両端支持ばりと、両端固定ばりで集中荷重がかかっている場合を示します。

 


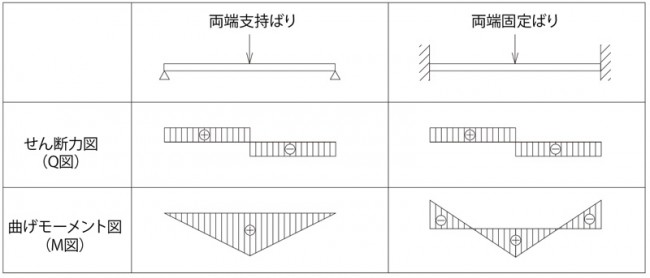
応力図

 

硬い金属だと感覚が掴みにくいかもしれませんが、

消しゴムのようなものを曲げると思ってみると解りやすいかと思います。

 

この応力図を見ると、せん断力が０のところで曲げモーメントが最大になっています。

両端支持ばりでは両端の曲げモーメントはゼロですが、

両端固定ばりでは両端に荷重が掛かっている中央部と同等の曲げモーメントがかかります。

 

両端固定ばりでは、曲げモーメントの符号が変わります。

つまりS字型に湾曲するわけで、両端から1/4の距離の点では曲げモーメントが０となります。

 

このように応力図で検討すると、部材をつなぐ場合など、

どの位置でどのような方法でつなぐのが良いかなど解りやすくなります。

 

 

博士「どうじゃ、あるる。応力の話はわかったかの？」

あるる「はい！　面白いですねー。

応力ってものがないと、物体はひっぱるとちぎれてぶっ飛んじゃうんですね。

そんな風に考えたことがなかったです。」

あるる「もしや博士、お昼のとき、この応力を考えながら割り箸を割っていたんじゃ…」

博士「わしの場合は、考えるというか、もうすっかり見に付いているというか…」

あるる「博士、スゴイ！　スゴすぎです！　博士にとっては日常も科学なんですね！」

博士「いや、それほどでも… (〃∇〃)」

あるる「これはひとつの才能・・・というより、超能力に近いかもっ?!」

博士「なんじゃ、あるる。またダジャレか。超応力、なんちゃって」

あるる「もう、博士ったら。マジメに感動していたのにぃ〜、もう（ぷん）」

博士「それは悪かったのぅ、ふぉっふぉっふぉっ（笑）」

あるる「（笑）」