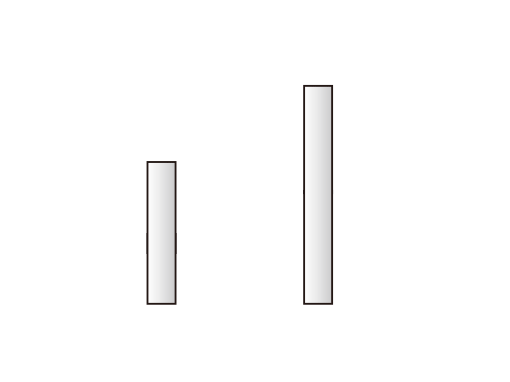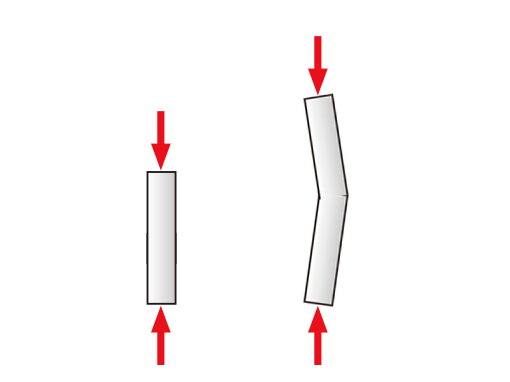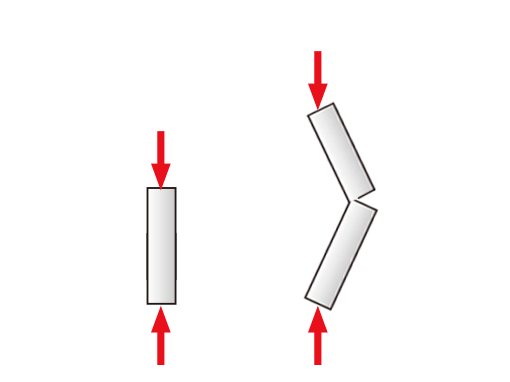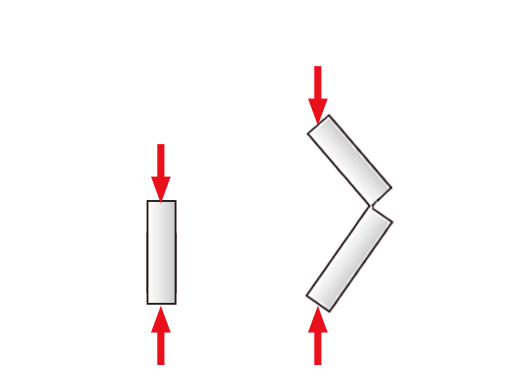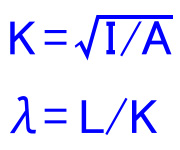みなさん、こんにちは。基礎用語、案内役のあるるです。
今回注目する基礎用語は、コチラ！
↓↓↓
今月の基礎用語：サ　＃041
座屈（ざくつ）
buckling

あるる「博士ぇ〜、昨日の棒高跳び世界一を決める試合、ご覧になりましたか〜？　すごかったですねぇ〜

博士「もちろんじゃとも。まさに手に汗握る大接戦じゃったのぅ」

あるる「はいっ！　人ってあんなに高く飛べるんですね。それにしても、あの棒のしなり！　いつポキっと折れるかと、ハラハラしちゃいましたよ」

博士「細くて長いモノほど、少しの力で折れたり変形するものじゃ。あの“しなり”を実現するのは、ある意味『座屈』との戦いともいえるのぅ」

あるる「ん？　ざくつ・・・？　なんか聞いたことあるような・・・」

博士「なんじゃ、キレイに忘れてしまったのか？　では、オイラーの法則は？」

あるる「『おいらはドラマ－』なら知ってますが・・・」

博士「ふぉっふぉっふぉっ、さすがおじいちゃん子。シャレが昭和じゃのぅ（笑0」

あるる「えへへ」

博士「よしっ！　では今日は『座屈』のおさらいじゃ！　これがわかると、今の棒高跳びがいかにスゴいことをやってのけているかがわかって、よりスポーツが楽しめるぞ」

あるる「そうなんですね！　よろしくお願いしますっ！！」

近年では太くて丈夫な柱や、厚い板を使わずして強度的に優れた材料がたくさんあり、構造物の軽量化やスリム化ができるようになりました。

しかし、条件によっては、材料の強度とは無関係に材料本来の強度よりもはるかに小さな力で急に変形の模様が変化し、大きなたわみを生ずることがあります。

この現象を「座屈」と言いますが、なぜこの様なことが起こるのでしょうか？

今回はこの座屈についてお話しましょう。

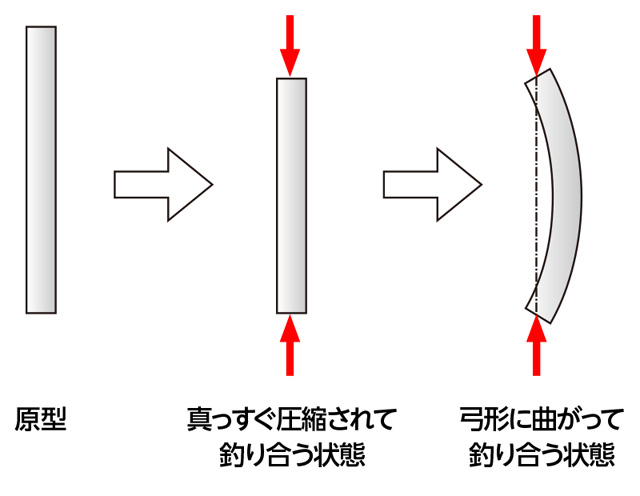
構造物に圧縮方向の荷重がかかった時に、ある時点で急激な形状変化が発生して、大きな変形や破壊を起こすことがあります。

短い部材に比べ、細長い部材は引張力より圧縮力の方が弱く、材料が持つ強度より遥かに小さな力で破壊します。

細長くまっすぐな棒の両端を押すと、力が小さいうちは単純な圧縮応力とひずみを生じて釣り合っていますが、

圧縮力がある値に達すると、釣り合いは急に不安定となり、棒は曲って耐荷力は急激に低下します。

このように、ある釣り合い状態（真っすぐ圧縮されている）から急激に別の釣り合い状態（弓形に曲がる）に変化することを「座屈」といいます。

なぜ軸力をかけたときに縮むのではなく、曲がるのか？

それは完全にまっすぐではなく、材料が均質ではないことによります。

ですから、部材がどれくらいまっすぐなのか、どれくらい均質なのかを数値で定めることが難しく、理論値に対してある安全率を見ることが必要なのです。

座屈の計算には、オイラーの公式、ランキンの公式、テトマイヤーの公式、ジョンソンの公式などがあります。

座屈が発生するときの荷重を「座屈荷重」といい、その時の応力を「座屈応力」といいます。

材料が極めて短い場合には、許容荷重は圧縮応力そのもので、これが上限値となりますが、

細長くなるほど、座屈が起きやすくなるので圧縮される構造物を設計する際は注意が必要です。

座屈荷重を求める際には、部材の細長さを表す細長比（λ）という値があり、値が大きいほど細長い構造であることを示します。

まずは最小断面二次半径（k）を求め、それから細長比を求めます。

λ：細長比

k：最小断面二次半径

L：座屈長さ

I：断面二次モーメント

A：断面積

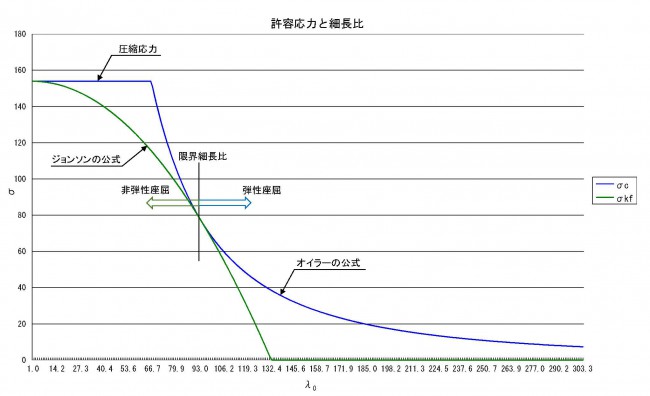
この細長比（λ）には限界細長比という値があり、限界細長比は概ね100程度です。

この限界細長比を境とし、限界細長比以上を弾性座屈、限界細長比以下を非弾性座屈といいます。

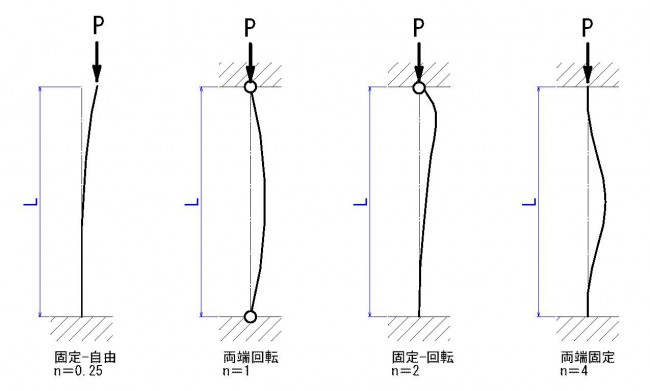
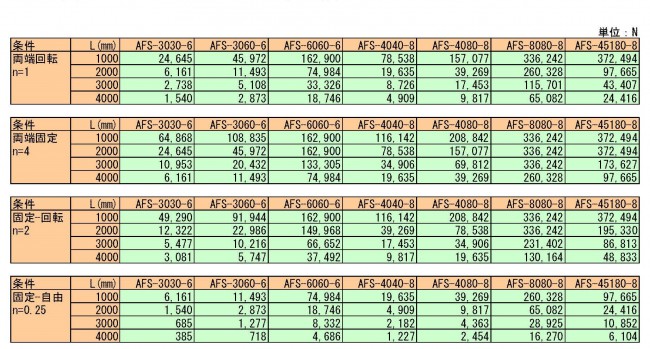
また、座屈荷重は支持条件によっても変わり、端末条件により、下図のような端末係数があります。

端末係数ｎを見てわかる通り端末条件により、許容応力は大きく変わります。

弾性座屈においてはオイラーの公式、非弾性座屈においてジョンソンの公式を用います。

その式を以下に記します。

長柱の座屈

オイラーの公式を見てわかる通り、座屈荷重は柱の長さの２乗に反比例するため、長いものは特に座屈しやすくなるので設計時は注意が必要です。

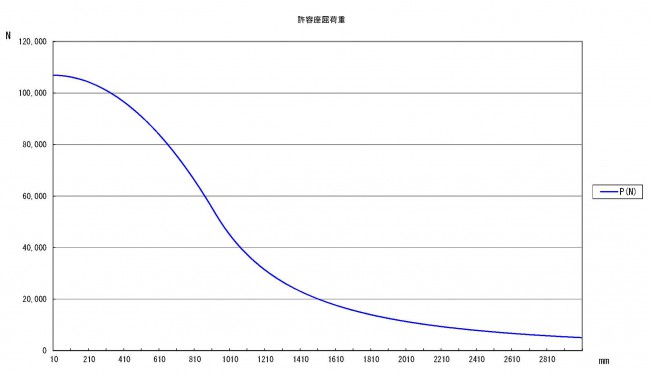
上記の式により当社アルファフレームAFS-3060-6を計算した結果を、グラフとして以下に示します。

許容応力と細長比

許容座屈荷重

参考として、以下に代表的なフレームに関する座屈計算結果を示します。

代表的なフレームに関する座屈計算結果

この値に適切な安全率を考慮して、設計を行ってください。

博士「どうじゃ、あるる。少しは思い出したかの？」

あるる「はいっ！！　計算は難しいですが、理屈はわかりました！」

博士「座屈の理屈か（笑）　今日は冴えているでじゃないか」

あるる「えへへ、それほどでも〜」

博士「棒高跳びのポールは、もともとは竹を使っていたそうじゃ。今は素材はもちろん、荷重がどうかかるかなどを研究し、折らずにあそこまでしならせるのじゃから、これぞ科学とスポーツの融合じゃな」

あるる「そうなんですね！　なんかスゴい！」

博士「少しでも良い結果を出そうという意味では、我々技術者も選手と一緒に戦っているといえるのぅ」

あるる「すごい！ロマンですね！！　よーし、帰ったら録画をもう一回見て、ポールのしなりを堪能しますっ！　では博士、さようなら！」

博士「さよう・・・もう行ってしまったか・・・　スガスガしいほどに一直線じゃのぅ」」