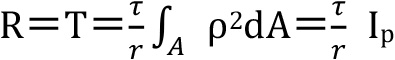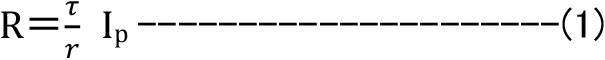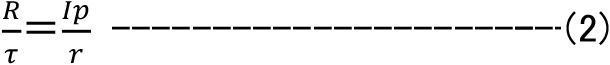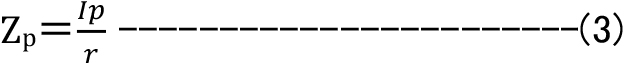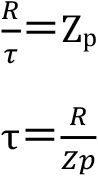みなさん、こんにちは。基礎用語、案内役のあるるです。
今月注目する基礎用語はコチラ！！
↓↓↓
今月の基礎用語：キ＃024
極断面係数（きょくだんめんけいすう）

polar sectional coefficient ／polar modulus of section

♪♪ ちゃんちゃかちゃかちゃか〜・・・♪♪

博士「よっ！　ほっ！」

あるる「おはようございます。博士、今日も朝から元気ですねぇ」

博士「おお、あるるも一緒にやらんか、ラジオ体操」

あるる「はいっ！！」

あるる「3年前を思い出しますねぇ。ねじる運動から『極断面係数』の話になって・・・」

♪♪腕を振って、カラダをねじる運動〜〜〜♪♪

あるる「あっ！　早速来ましたね！！」

博士「ほっ！　ほっ！」

あるる「いよっ！　はっ！」

博士「あるるよ、ねじりが上手くなったではないか」

あるる「はいっ！　毎日練習して『極断面係数』高くなりました〜♪」

博士「えらいぞ、あるる。日々の積み重ねが大切じゃ。よし、体操が終わったら、『極断面係数』の復習じゃ！」

あるる「はいっ！！」

極断面係数は、断面二次極モーメントと同様に、断面形状からその材料のねじれ強さを表すものです。

断面二次極モーメントは、ねじれ量を算出するときに、極断面係数は応力度を算出するときに使います。

言い換えると、ねじりモーメントに対して

断面二次極モーメントは、どれだけねじれにくいか
極断面係数は、ねじれにどれだけ耐えれるか

を表す数値で、両方とも材質には関係がなく、断面形状の性能を表すものです。

まず、前号の式（10）

R：ねじり抵抗モーメント
T：ねじりモーメント（トルク）
τ：ねじり応力
Ip：断面二次極モーメント

ここで、Ipとrの関係で表されるのが、極断面係数Zpです。

第87回「【今月のまめ知識 第87回】断面係数」で断面係数を説明しているので、それを理解していると、よりわかりやすと思います。

式（2）(3)より

となります。

このτがねじり応力ですが、ねじり抵抗モーメント(R)を極断面係数(Z_p)で除した値であり、

極断面係数(Z_p)は、断面二次極モーメント(I_p)を半径(r)で除した値です。

つまり、断面二次極モーメントと同じく、材質には全く関係のない値です。

断面二次極モーメントの単位はmm⁴でしたが、
極断面係数はそれを長さで除しているので単位は、mm³となります。

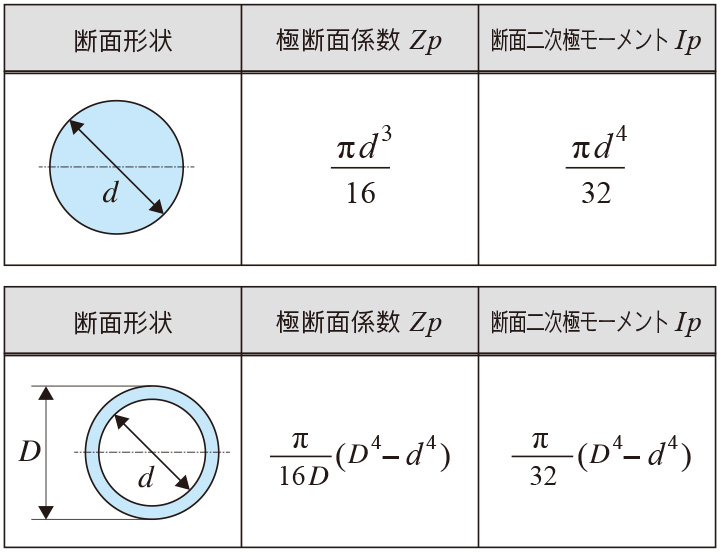
前回の式(2)で円形断面の断面二次極モーメントを示しました。

　I_p=πD⁴/32

極断面係数はこれをr(=D/2)で除したものなので

　Zp＝πD³/16

となります。

つまり中実軸の場合に、軸のねじれにくさ（ねじり剛性）は軸径の4乗に比例し、
軸の破壊しにくさ（ねじり強度）は軸径の3乗に比例するわけです。

このことから、ねじり剛性については、中実軸より中空軸が軽量で有利なことがわかります。

中空軸は、外径の値から中空径の値を引いた値となるので、まとめると以下のようになります。

実は前回、今回で説明したねじりに関することは、円形断面に限られます（円形断面とは、中実円、中空円、中実楕円、中空楕円）。

矩形断面などそれ以外の形状においては、弾性学となり、断面の湾曲のため、そのせん断応力は辺の中央部で最大になり、4隅の角では、0となります。

イメージで言うと、ゴムの丸棒をねじると外周で応力が最大になりますが、長方形断面のゴムの角柱をねじると広い面の中央部（中心から一番近いところ）が最も湾曲することが想像できるかと思います。ここで応力が最大となるわけです。

さらに、開断面形状（H鋼やナット溝のあるアルミフレーム）ではまた異なった挙動となります。

これらについては改めて説明いたします。

あるる「やっぱり復習って大事ですねぇ。前回より計算式を見ても、ビビらなくなりました」

博士「そうか。それが成長の証じゃ」

あるる「ありがとうございます。そして博士、見てください！　」

博士「お、おおおーーーっ」

あるる「こんなに捻れるようになりました！！（ぐぃーん）」

博士「おおお、素晴らしい！　見事な極断面係数の高さじゃ！！！」