うとうとしていたあるるの耳に、突然妙な音が聞こえてきた

ブィ〜ン　ブィ〜ン　ガタガタガタ　・・・

あるる「ひっ！（驚）（じゅる←ヨダレを拭く音）な、なんだ？」

ガタガタガタ　ブィ〜ン　ブィ〜ン　・・・

あるる「おや、博士のスマホだ。あ〜、びっくりした。博士ぇ〜、スマホ、スマホが鳴ってますよぉ〜！」

博士「おお、すまんすまん。机に置きっぱなしじゃったか。えっと、どこじゃ、どこじゃ」

あるる「その書類の下ですよ。あー、切れちゃった。こんなに散らかすからですよ。

普段から整理整頓が大事なんじゃないんですか（チラ）」

博士「いやはや、面目ない。今、研究の真っ最中でな（ぽりぽり）」

あるる「もう、博士のスマホのおかげで、すっかり目が覚めちゃったじゃないですか。

せっかくいい気持ちでお昼寝してたのに・・・」

博士「すまん、すまん。でも、寝坊助あるるを起こすとは、我がスマホは優秀じゃのう（笑）」

あるる「もう、博士ったら！」

博士「そうじゃ。お前を起こしたバイブ、つまり「振動」じゃが・・・」

あるる「もちろん知りませんよ（きっぱり）」

博士「まだ何も言っておらんが・・」

あるる「話したいんでしょ？　振動について。了解でーす。お願いしまーす」

博士「また先回りしおって・・・。目覚めが悪かったのかのぅ」

振動とは、平衡な点を中心として周期的な運動を繰り返す状態です。

振動には以下の要素があります。

振動数（周波数）：1秒間の往復回数

振幅（変位）：往復している幅

速度

加速度

剛性が高いほど振動数は高くなります。

10Hz以下の低周波ではその揺れは目視可能で、ゆらゆらという感じです。

10～1000Hzは目視出来ないですが、手で触れると解る範囲で一般に機械の振動はこの範囲です。

1000Hz以上では触れても感じることは困難で、振動と言うより異音の領域になります。

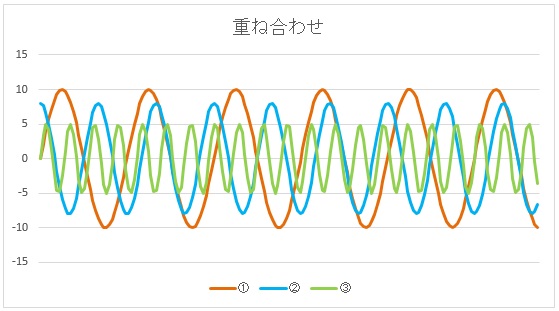
機械は色々な振動が複合しており、その変位を測定すると以下のような複雑な波形が出てきます。

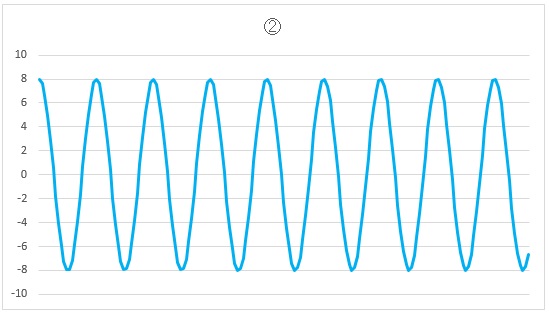
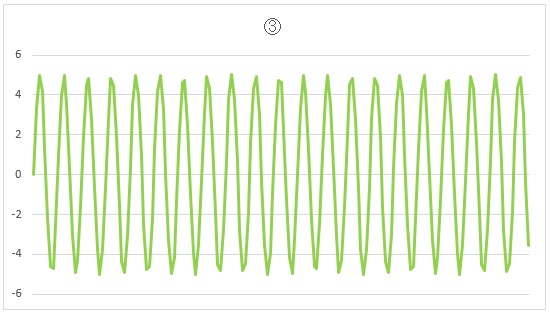
大変複雑な波形ですが、どのような波形も複数のsinとcosに分解できます。

振り子や、ばねに吊るした重りの振動がsinカーブとなる事は皆さん承知の通りですが、

すべての振動はこの組み合わせです。

複雑な波を分解し、周波数ごとに分けるのが“フーリエ変換”（FFT）です。 

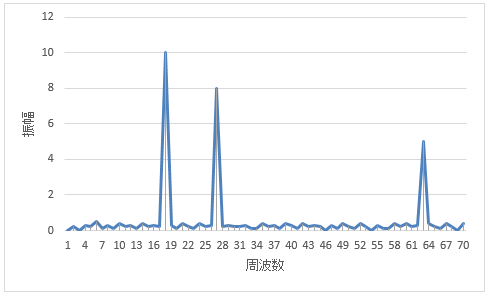
上図の波形をFFT解析すると、以下のようなパワースペクトル（周波数バンド幅毎のパワー）が求められます。

（イメージ図）

そして、それぞれの周波数の波形は以下のようになります。

これらを重ね合わせると以下のような波となり、この①②③の波を合成すると元の測定した波形となります。

ちなみに剛性の高い装置架台というのは、固有振動数の高いフレームです。

振幅、固有振動数、加速度は互いに関係があり

振幅（変位量）は固有振動数の2乗に反比例し、加速度に比例します。

実際に評価を考える時に具体的に一番分かりやすいのは

単純な寸法の単位であるｍｍで表される振幅（変位量）でしょう。

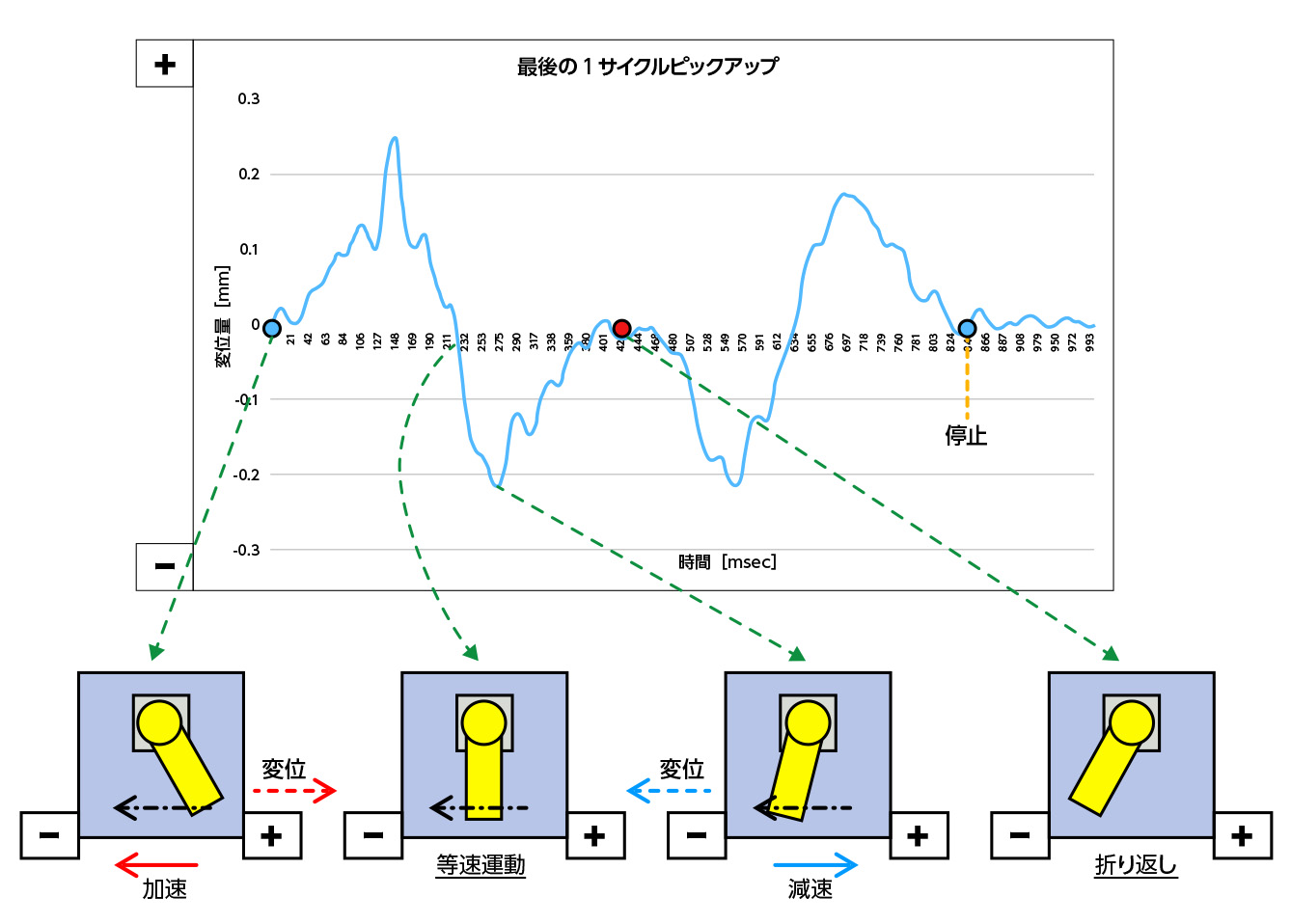
実際に、ロボットを架台に積載し以下のように変位量の測定を実施した結果を紹介します。

上図の条件でのX方向変位を測定したところ、以下のようになりました。

この波形を見ると、大きな波と小さな波が合わさっていることがわかります。

振動と言えるのは、30Hz程度で振幅0.02mm程度の細かい波です。

大きな波はロボットの動作位置と合わせてみると、ロボット動作の反力（荷重）による変位であることが解りますが、これは振動ではありません。

例えるならば、自動車で加速するとフロントが持ち上がり、減速するとフロントが下がるのと同じで、振動は継続的に車体に伝わっているものと考えれば区別がしやすいと思います。
（最近の乗用車では感じれませんが、古いトラックなどをイメージしてください）

いずれにしても、固有振動数を高くすれば大きな波である変位も、振動に寄る変位も両方抑えることができます。

従来、ロボット架台や装置架台は多くの場合、設計者の勘と経験にて設計されています。

1本の梁であれば、断面二次モーメントや断面二次極モーメントといったデータから算出できますが、フレーム構造体となった場合にはそれらを参考とすることは出来ても、ラーメン構造やブレスを加えた場合など、どの程度の剛性アップになるかを簡単に判断することは困難であり、解析に頼る事になります。

これは静的にはある程度の信頼性がありますが、動的には振動やその減衰という問題も有り、動的解析を手掛けるとなると大変難しいものになります。

今後、ロボットを使用するFA装置が増えていく中で、その精度とスピードを生かす装置架台の設計は目立たない部分ですが重要なものとなるでしょう。

博士「どうじゃな、あるる。なんだかポーッとしているように見えるが・・・　振動については理解できたかの？」

あるる「・・・振動の波形って、キレイなんですねー。特に3つの波形を重ねたところなんて、本当にキレイ・・・（うっとり）」

博士「なんじゃ、そこに食いつきおったか。まぁ、あるるらしいのぅ」

博士「きっかけはどこからでも良いぞ。そこから興味を膨らませてゆけば良いのじゃからな」

あるる「はいっ！　振動、面白いです！　もっと知りたいです！」

博士「感心、感心。よし、来年もしっかり学んでいくぞ」

あるる「はいっ！　振動を理解して、目指せ、神童！　なんちゃって」

博士「ふぉっふぉっふぉ。お互い、良い年を迎えような」