みなさん、こんにちは。基礎用語、案内役のあるるです。
今回注目する基礎用語は、コチラ！
↓↓↓
今月の基礎用語：コ　＃035
構造解析
structural analysis

あるる「うんしょ、うんしょ・・・」

博士「おや、あるる。一生懸命、何を書いているのだ？」

あるる「あ、博士！　もうすぐ夏休みなので、棚を作ろうと思って・・・」

博士「まだ休みにもなっていないのに、随分と気が早いことじゃのぅ（笑）」

あるる「てへへ。昨日、おじいちゃんが盆栽を置く棚があったらなぁ・・・って呟いていたのを偶然聞いちゃったんです。ならば、あるるが作って、サプライズしようと思いつて」

博士「えらいっ！　えらいぞ、あるる！　ならば丈夫な棚を作らなければな！」

あるる「そうなんです。結構大きな鉢もあるので、重さに耐えられるものを作らないと」

博士「よし、全面協力しようではないか！　まずは解析じゃ！」

あるる「えっ？！　懐石？！　博士も気が早いですねぇ。ご褒美は完成したらでいいですよ〜〜〜」

博士「え？　もしや懐石料理のことを言っているのでは？」

あるる「え？　違うんですか？」

博士「その懐石”ではない。“解析”じゃ。・・・って、このやりとり、以前もしたような（笑）」

あるる「はい、確かに。懐かしいですねぇ（笑）」

博士「なにはともあれ、早速始めようぞ！」

構造解析とは、構造物や物体に荷重をかけたときに、どのように変形し応力る発生するかを計算して数値化し、評価・分析する方法です。

当社ではご要望に応じて、最適設計化のための構造解析を行っております。

解析を行うケースとしては

・大きな荷重がかかる構造物の、部材，構造検討
・ロボットによる動作がある構造物の、部材，構造検討

などですが、以下のことを検討していきます。

• 部材にかかる応力や変位量を求めて要求仕様を満たすか
• 不可の場合にはどのように改善するか
• 過剰な剛性をもつ場合にはどこを削減するか　　など

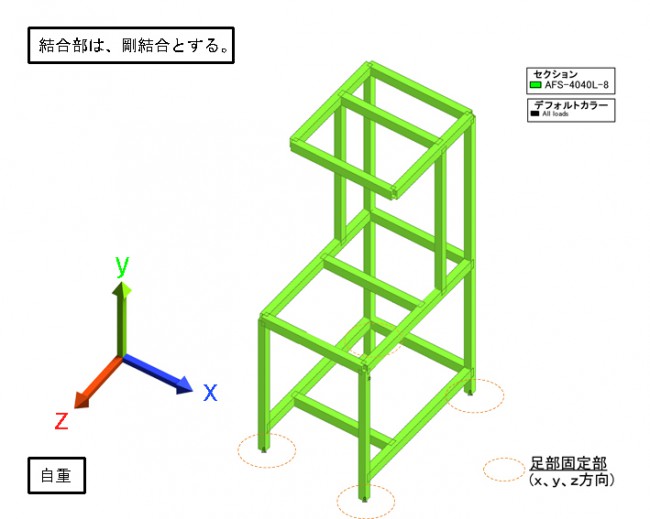
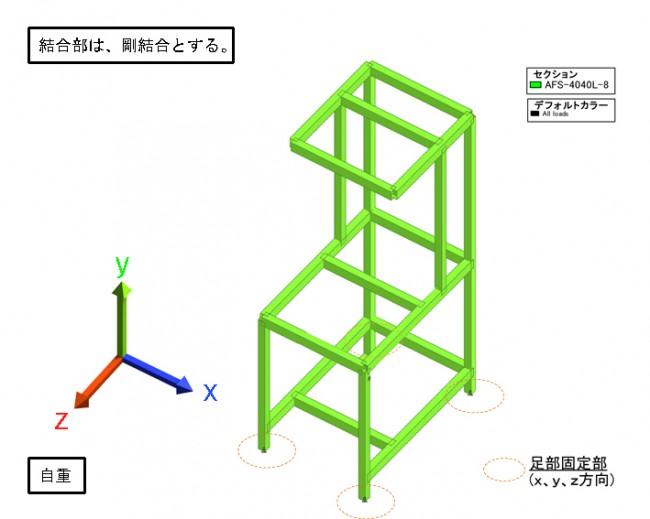
ご提示いただくものは、

・フレーム構造図
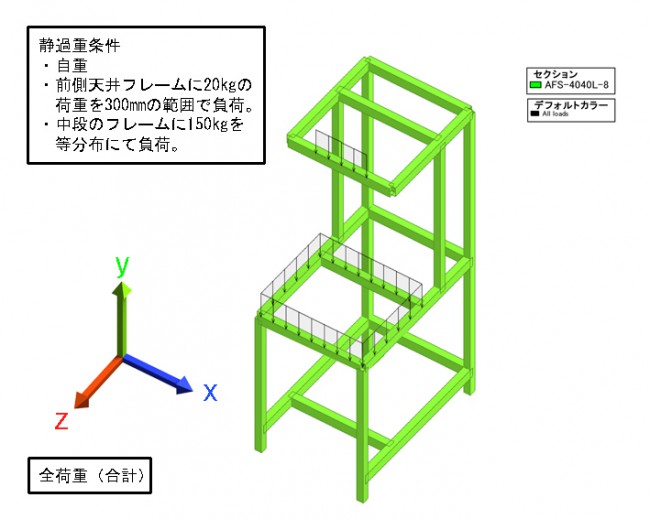
・積載される機器の質量とその部位
・大きな動きがある場合はその位置と質量と加速度
・必要な剛性（安全率，指定位置の変位量など）

となります。

解析手順は、次の通りです。

【1】フレーム構造を図のようにワイヤーモデル化し、各節点に節点番号が付きます。

【2】そのワイヤーモデルに指定荷重を付加します。

そして以下の値が解析結果として得られます。

①変位

・dx、dy、dz

各節点でのそれぞれx,y,z方向の変位量です。

各方向は変位図左下にある図示の通りで矢印方向がプラスとなります。

ワイヤー図に示された節点番号ごとに表記されます。

【変位値】サンプルモデル解析結果（クリックで拡大）

②応力度

応力度】サンプルモデル解析結果（クリックで拡大）

・Sbx、Sby、Sbz

各節点でのそれぞれx,y,z方向の曲げ応力です。

各方向は変位図左下にある図示の通りで矢印方向がプラスとなります。

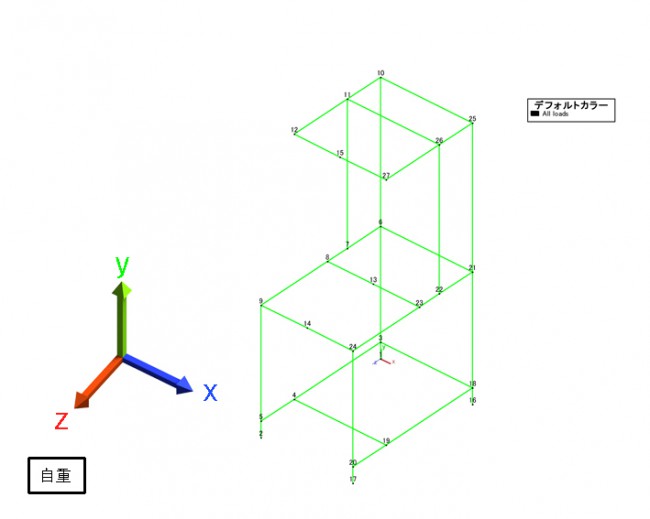
ワイヤー図に示された部材番号，節点番号ごとに表記されます。

・Sx、Sy、Sz

各節点でのせん断力です。

方向は図示のx,y,zとは無関係です。

それぞれの部材の軸方向がx、軸直角方向上下がz、左右がyとなります。

ワイヤー図に示された部材番号，節点番号ごとに表記されます。

・Sx+Sbz，Sx+Sby

各節点でのせん断応力と曲げ応力の合成応力です。

方向は図示のx,y,zとは無関係です。

それぞれの部材の軸方向がx、軸直角方向上下がz、左右がyとなります。

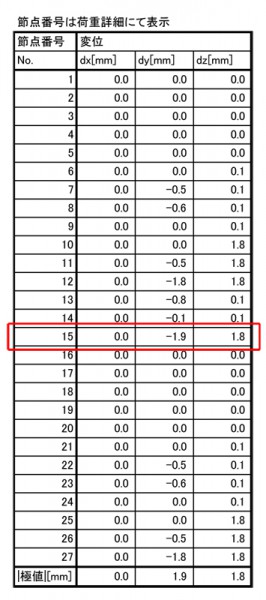
今回のサンプル架台の極値は、変位図に記載しましたとおり、

節点番号『15』に、y方向変位極値（1.9mm）z方向変位極値（1.8mm）

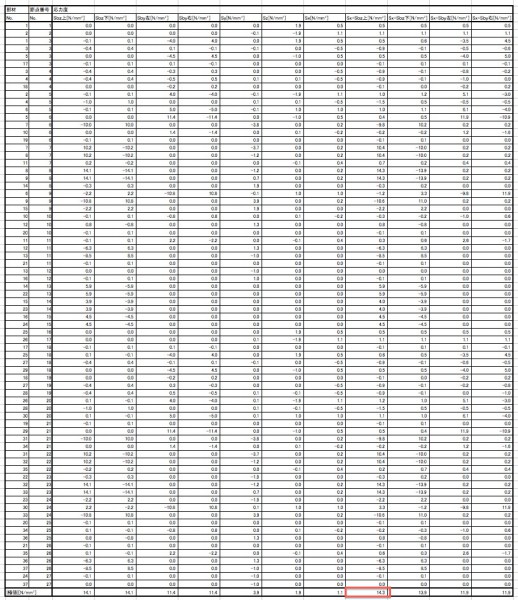
節点番号『8』に、応力極値（14.3N/mm²）

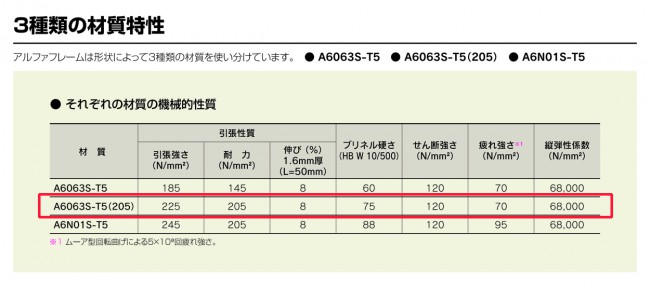
アルミフレームの機械的性質は、以下の通りになります。

ここで許容応力の考え方ですが、アルミニウム合金においては前号でもお話したとおり、耐力値の75%を弾性限度と考えます。

205N/mm2×0.75＝154 N/mm2

仮に安全率3で考えると

154N/mm2÷3＝51 N/mm2

今回の応力極値と比較すると

14.3N/mm²＜51 N/mm2

ですから、このサンプル架台は、応力に関して十分に安全性が高いと言えます。

変位量については、要求される数値との比較になります。

これらの結果に基づいて、主要部材の強度を落としたライト級に変更した場合の再解析を行い、結果を見てコストダウンをご提案するケースも多くあります。

この様に最も高い応力値が使用条件に対して適切な安全率を持つかどうかを判定します。

X,Y,Z各方向の最大変位点とその変位量を確認し、指定点の変位量が指定条件以下であるかどうかを判定します。

博士「どうじゃ、あるるよ。解析の奥の深さ、思い出したかの？」

あるる「はい！　相変わらず計算は難しいですが、改めて“解析スゲェ！”と思っています」

博士「ふぉっふぉっふぉっ。以前もそんなことを言っておったのぅ」

あるる「丈夫にするためにモリモリすぎてもダメだし、逆にスカスカは問題外だし、最適な設計ってところが肝なんですね」

博士「おっ、わかっておるではないか。やっぱりちゃんと成長しておるんだのぅ。よしよし。うれしいではないか」

あるる「ありがとうございます！！」

博士「よし、そこがわかったのなら、おじいちゃんのため、最適な棚を作るのだぞ。具体的にはここをこうしてな・・・」

あるる「ふむふむ、なるほど・・・　さすが博士！！　完成したら何かお礼をさせてください！！」

博士「ほう、そうか。それなら遠慮なく、懐石料理でもご馳走になろうかのぅ（にやっ）」

あるる「え？！　お小遣い、足りるかな・・・」

博士「お弁当で十分じゃ」

あるる「ほっ（よかった〜〜）。それなら大丈夫です。お任せください！！」