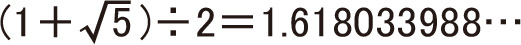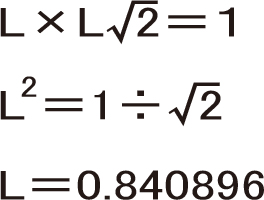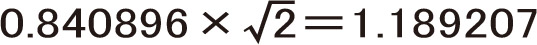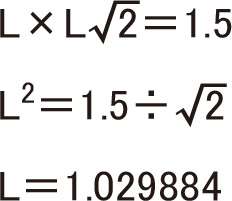いまさら聞けない基礎用語【オ】#010 黄金比
公開日時:2022/06/29
黄金比(Golden ratio)
みなさん、こんにちは。基礎用語、案内役のあるるです。
今回注目する基礎用語は、コチラ!
↓↓↓
今月の基礎用語:オ #010
黄金比(Golden ratio)
あるる「今日も色とりどりで綺麗だなぁ〜♪ ルンルンルン♬」
博士「おはよう、あるる。今日も朝からご機嫌じゃな」
あるる「あ、博士、おはようございます。今日も紫陽花の花が綺麗に咲いてるなぁ〜っと思って♪
ほら、濃い紫に薄い紫、こっちは赤紫も! 花びら、かわいい〜♪」
博士「ほんに綺麗で、心が安らぐのぅ〜。でも、あるるよ。夢を壊すようでなんなんじゃが、これは正確には花ではないんじゃ」
あるる「えええ? なんですと?」
博士「『ガク(萼片(がくへん)』と呼ばれる葉っぱの部分が変形したものなんじゃ」
あるる「ええーーーっ!? 花じゃなくて、ガクーー?! わーー、びっくり、愕然!!(◎_◎;)」
博士「そんなに驚いてくれなくても(笑)」
あるる「じゃぁじゃぁ、花はどこにあるんですか?!」
博士「ガクの中に小さな蕾のようなものがあるじゃろう。それが紫陽花の花じゃ。かき分けて見てごらん。花びらは5枚じゃ」
あるる「なんと! さすが博士、ガク(学)があるぅ〜♪」
博士「びっくりしすぎて親父ギャグ炸裂か(笑)花びらの数といえば・・・?! 」
あるる「あっ! フィボナッチ!!」
博士「おお、覚えておったのか? えらいぞ、あるる」
あるる「ええ、【今月のまめ知識 第83回】規則性のある長方形の回で教えてもらってから、なんだか頭から離れなくて。一度覚えたら、何度でも言いたくなる言葉ですよね、フィボナッチ(笑)」
博士「その感性はよくわからぬが・・・まぁ、きっかけはなんであれ覚えてくれるのは、ありがたいぞ」
黄金比とは
そしてこの配列が、フィボナッチ数列と関係があるのです。
フィボナッチ数列は、前の2つの数を足した数が次の数となる数列で
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377・・・・・・・
と無限に続きますが、この隣り合う数の比は、黄金比に収束します。
55÷34=1.61764706…
89÷55=1.61818182…
144÷89=1.61797753…
233÷144=1.61805556…
377÷233=1.61802575…
となり、数値が大きくなるほど黄金比に近づいていきます。
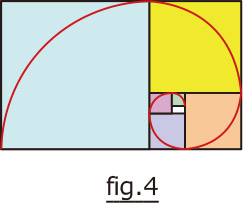
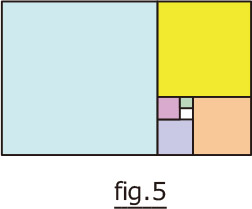
フィボナッチ数列を以下に図で示します。
fig.5で一番小さいホワイトとグリーンの正方形の1辺の長さを1とすると
次のピンクの正方形の1辺の長さは2、
その次のパープルの正方形の1辺に長さは3となります。
fig.4は黄金比の長方形を細かくして言っているので、細分化した長方形もすべて辺の長さの比は黄金比です。
fig.5の正方形を加えることを繰り返すと、fig.4の黄金比に近づきます。
このフィボナッチ数列は、自然界でたくさん見受けられることで知られています。
松ぼっくりやひまわりの種の配列、木の枝の成長の配置、巻貝の渦巻きなど、まさに、ガリレオ・ガリレイが「自然という書物は数学と言う言葉で書かれている」という言葉の一端を表しています。
自然を見て、美しさ、生命力、神々しさ、厳しさなど色々な感じ方がありますが、その規則性から数学的なものを感じるということ。
毎日の仕事では、このような規則性を見出すことが生産性向上に一役買うのではと考えます。
「白銀比」というものもある
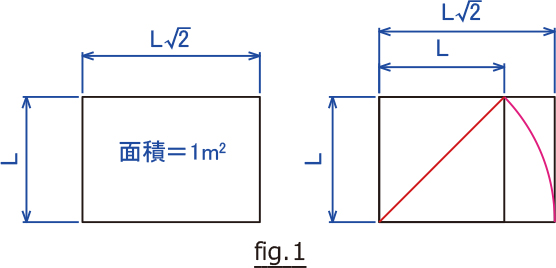
一般の用紙はA版とB版がありますが、どちらもルート長方形と言う形で短辺と長辺の比が、
A0は面積が1㎡、B0は面積が1.5㎡となる大きさです。
ルート長方形とは、正方形の対角線の長さを長辺とした長方形で、この比率を「白銀比」と言います。
A版用紙の寸法
規格寸法は、841mm×1189mmです。
A0の半分の面積がA1であり、そのまた半分がA2と続きます。
ですから、例えばA4の面積は
B版用紙の寸法
規格寸法は、1030mm×1456mmです。
B0の半分の面積がB1であり、そのまた半分がB2と続きます。
A版にしろ、B版にしろ、この規則性が原版の材料を無駄なく使い、整理もしやすいと言う合理性に基づいています。