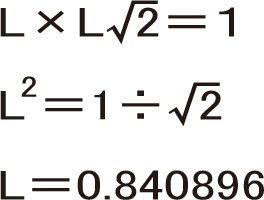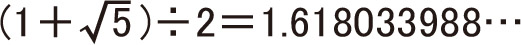あるる「ふふふんふん♪」
博士「おお、あるる。この寒空の中、掃き掃除とは感心じゃのぅ。」
あるる「あ。博士、おはようございます♪　毎朝おじいちゃんと一緒に掃き掃除しているので、
　枯葉を見ると、カラダが勝手に動いちゃって（笑）　キレイになるの、気持ちいいんですよ〜」
博士「感心感心。偉いぞ、あるる」
あるる「あっ！　梅が咲いてる！」
博士「ほんとじゃ。今年は少し早いようじゃがう〜ん、キレイじゃのう」
あるる「本当に。いい匂いだし。もうすぐ春、って感じですね♪」
博士「ところであるるよ。梅の花びらは何枚か知っているか？」
あるる「数えたことないなぁ〜。えっと、1、2、3・・・5枚です」
博士「正解。桜もナデシコも5枚。コスモスは8枚、菊は13枚、21枚、34枚などがあってな・・・」
あるる「へぇー、すごーい（棒読み）　シャッシャッ（←ほうきで掃く音）」
博士「フィボナッチじゃ！！」
あるる「へ？　へぼな・・・聞いてなかったからとといって「ヘボ」はひどくないですか？」
博士「ふぉっふぉっふぉっ。ヘボではない。フィボ、フィボナッチじゃ」
あるる「なんですか？　それ？　美味しいんですか？」
博士「これがわかると、「もののかたち」がもっと楽しくなるぞ。
　よし、授業開始じゃ！　さぁ、ほうきを片付けて！」
あるる「ああ、火がついちゃった。でも、なんだか面白そう・・・♪」

一般の用紙はA版とB版がありますが、どちらもルート長方形と言う形で短辺と長辺の比が、

A0は面積が1m²、B0は面積が1.5m²となる大きさです。

ルート長方形とは、正方形の対角線の長さを長辺とした長方形で、この比率を「白銀比」と言います。

試しにA0の寸法を算出してみましょう。

となり、長辺は

規格寸法は、841mm×1189mmです。

A0の半分の面積がA1であり、そのまた半分がA2と続きます。

ですから、例えばA4の面積は

となります。

つづいてＢ版は、

となり、長辺は

規格寸法は、1030mm×1456mmです。

B0の半分の面積がB1であり、そのまた半分がB2と続きます。

A版にしろ、B版にしろ、この規則性が原版の材料を無駄なく使い、整理もしやすいと言う合理性に基づいています。

では次に、似たような作図でできる黄金比について説明します。

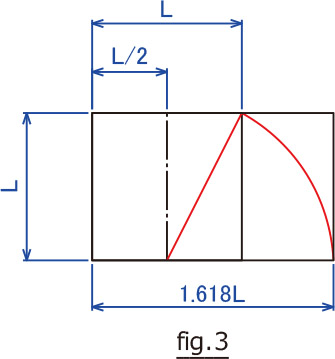
正方形の底辺の中点から円弧を描いて底辺の延長線との交点までを長辺とした長方形を描くとこの長さは、1.618 Lとなります。

この、1：1.618が黄金比（黄金分割）です。

これを計算で出すと

となります。

この正方形部分を除いた右側部分の長方形も黄金比となっており、ここからまた正方形を取り除いた残りの部分も黄金比となります。

そしてこの配列が、フィボナッチ数列と関係があるのです。

フィボナッチ数列は、前の２つの数を足した数が次の数となる数列で

0,1,1,2,3,5,8,13,21,34,55,89,144,233,377・・・・・・・

と無限に続きますが、この隣り合う数の比は、黄金比に収束します。

　　　55÷34＝1.61764706…

　　89÷55＝1.61818182…

　　144÷89＝1.61797753…

　　233÷144＝1.61805556…

　　377÷233＝1.61802575…

となり、数値が大きくなるほど黄金比に近づいていきます。

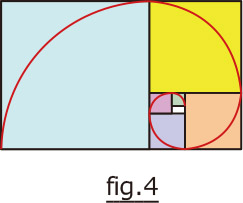
フィボナッチ数列を図示すると

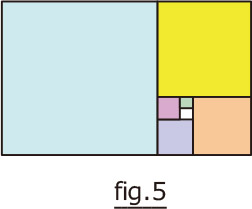
fig.5で一番小さいホワイトとグリーンの正方形の1辺の長さを1とすると

次のピンクの正方形の1辺の長さは2、

その次のパープルの正方形の1辺に長さは３となります。

fig.4は黄金比の長方形を細かくして言っているので、細分化した長方形もすべて辺の長さの比は黄金比です。

fig.5の正方形を加えることを繰り返すと、fig.4の黄金比に近づきます。

このフィボナッチ数列は、自然界でたくさん見受けられることで知られています。

松ぼっくりやひまわりの種の配列、木の枝の成長の配置、巻貝の渦巻きなど
まさに、ガリレオ・ガリレイが「自然という書物は数学と言う言葉で書かれている」という言葉の一端を表しています。

自然を見て、美しさ、生命力、神々しさ、厳しさなど色々な感じ方がありますが、その規則性から数学的なものを感じるということ。

毎日の仕事では、このような規則性を見出すことが生産性向上に一役買うのではと考えます。