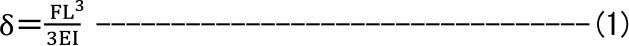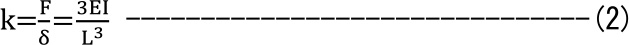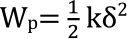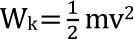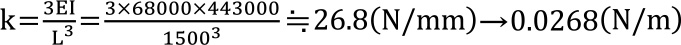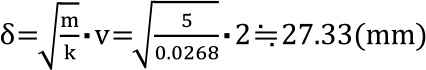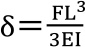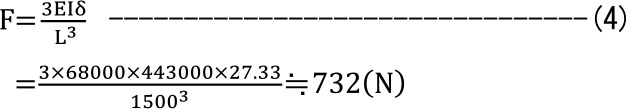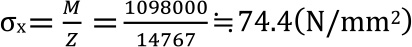博士「おはよう、あるる。どうしたのじゃ、その頭の大きな絆創膏は？」

あるる「おはようございます。あ、これですか？　昨夜、ちょっとぶつけちゃって・・・」

博士「おやおや、気をつけるんじゃぞ。どこにぶつけたんじゃ？」
あるる「家の・・・柱です」

博士「なんと！（笑）」

あるる「我が家では昨夜から、お風呂あがりのアイスが解禁になったんです。
　それだけでも嬉しいのに、なんと、記念すべき初アイスが「当たり」だったんですよ！！！」

博士「・・・ほう・・・」

あるる「もっと反応してくださいよ！　すごいことでしょう！？　ね、ね」

博士「そうじゃのう・・すごいのう（棒）・・・で、どうしたのじゃ？」

あるる「あんまりうれしかったので、めっちゃテンション上がってダンシン♪ダンシン♪
　「喜びの舞」のクライマックスで・・・！！」

博士「ぶつけたんじゃな（笑）」

あるる「正解（笑）。おかげで、たんこぶできちゃいました（＞＜）」

博士「まったく。あるるらしいというか・・・。ぶつかった衝突は、結構なものだったろう」

あるる「はい。目から火が出て、一瞬真っ白になりました」

博士「よし、どのくらいの力がかかったか、さっそく計算してみようぞ」

あるる「なぬ？　計算？　そんなことできるんですか？！」

博士「（にやっ）もちろんじゃ♪ 

あるる「博士、すごーーーい・・・（呆然）」

アルミフレームの柱に物体が衝突した場合の強度に関して考えたいと思います。

フェンスやマシンカバーなどは色々なものが衝突する可能性があります。
人がぶつかった場合、ロボットアームが当たった場合、ロボットハンドからワークが外れて飛んできた場合などが考えられます。

それらは衝撃荷重であるケースが多いので、その剛性検討は難しいものとなります。

金網や樹脂カバーへの衝突の場合などは、そこでそれが破壊したり脱落したりすることもあり、またそれが耐えた場合にはそこで衝撃を吸収するため、支えている柱への荷重は緩和されます。

今回は純粋に1本の柱に物体が衝突した場合を、出来るだけ単純な理論で計算してみたいと思います。

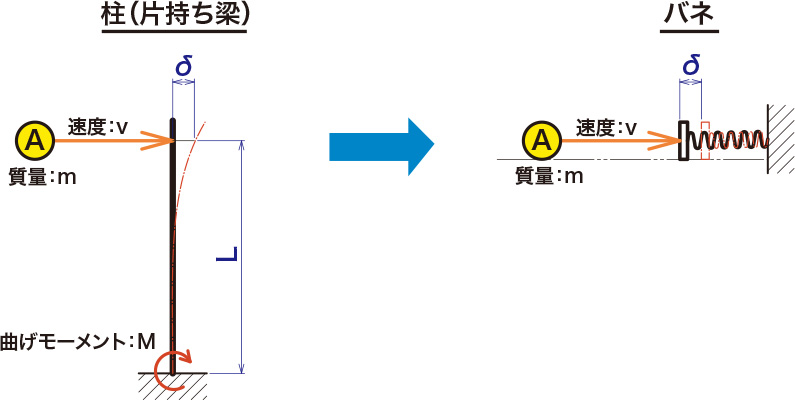
質量mの物体Aが速度vで下部がしっかり固定された1本の縦柱に衝突したとします。

条件として反発係数を0として考えます。

反発係数を説明しておくと、ボールをある高さから床に落としたとき衝突直前と衝突直後において、速さが同じ（元の高さまで跳ね返る）場合が１となり、衝突直後の速さが0となる（全く跳ね返らない）場合が反発係数0です。

物体Aが柱に衝突しても跳ね返らずに密着して柱を押していく想定で、実際には速さは0ではないですが跳ね返りではないので反発係数0と考えます。

まず柱をバネと考えて、バネへの衝突としてモデル化します。

柱は片持ち梁であり、板バネと仮定してバネ定数を算出します。

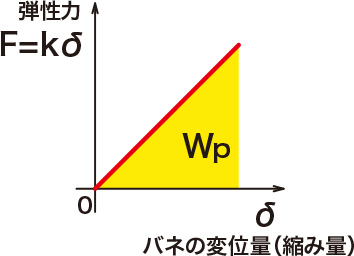
この衝突による柱の変位量が、あくまでも材料の弾性限度内であるという前提で、弾性力による位置エネルギーを考え、図のバネモデルでのすべり面の摩擦は無視します。

そして、運動してきた物体Aが停止するという事は、物体Aの運動エネルギーがゼロになってバネの位置エネルギーに変換されたと言うことになります。

まず、片持ち梁のバネ定数を求めます。

片持ち梁のたわみは

バネ定数kは

次に弾性力の位置エネルギーを求めます。

バネはフックの法則により変位量δと弾性力Fが比例するので、仕事＝力×距離であり、仕事はエネルギーと同じ単位で変換できます。

つまりこのグラフのWpの面積が、弾性力の位置エネルギーとなります。

そして物体Aの運動エネルギーは

物体Aの運動エネルギーがすべてバネの位置エネルギーに変換されたとし、熱エネルギー等へのロスは無視すると、Wp=Wkとなるので

これをδで解くと

となります。

具体例で計算してみましょう。

物体Aの質量と速度を以下と想定 

　m＝5kg

　v＝2 m/sec

 柱はAFS-6060-6で、衝突部の高さを1.5mとすると

　E＝68000N/mm²
　I＝443000mm⁴
　L＝1500mm

まずkを求めます。式(2)より

δを求めます。式３より

となります。

δはつまり片持ち梁の変位量となるので、この時の荷重Fを求めることが出来ます。

片持ち梁のたわみ算出の式(１)

より

となります。

式(2)で柱のバネ定数を求め
式(3)で衝突部の最大変位量を求め
式(4)で衝突部が受ける最大荷重が求まるわけです。

次に許容荷重内であるか確認しましょう。

豆知識第87回【断面係数】参照

AFS-6060-6の断面係数は

Z＝14767mm³

この事例での柱の根元の曲げモーメントは

M＝F×L＝732×1500＝1098000(Nmm)

となり、応力は

材料の耐力値205N/mm²、弾性限度はその75%で154N/mm²であり、この事例は許容応力内と言えます。

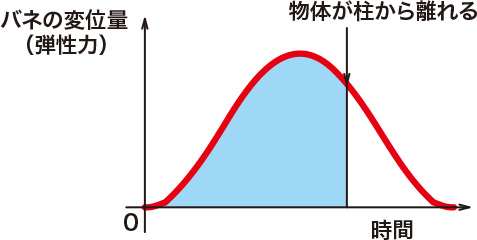
実際に衝突はもっと複雑であり、時間と加速度（受ける荷重）の関係で考えると
衝突物の変形もあり、台形波形で等加速度運動に近い状態になる場合や、sinカーブのように徐々に加速度が高まる場合も考えられます。

また、下図に示したように梁がたわんで荷重が大きくなり衝突物体の運動エネルギーより梁の弾性力の位置エネルギーの方が大きくなると、バットでボールを打ち返すように柱が戻り始め、戻りきる前に衝突物を跳ね返すという動きにもなります。

柱が水平で物体が鉛直方向に落下してきた場合などに考えられますが、この場合はこの柱の位置エネルギーが衝突物に運動エネルギーを与えたという事になります。

このように色々なケースが考えられますが、今回のような単純な計算で最適な設計をする目安になればと思います。

博士「どうじゃ、あるる。わかったかの？」

あるる「パチパチパチパチ・・・（拍手）　すごーい。こうやって計算するんですね。目からウロコが落ちました」

博士「目の前が真っ白になったり、ウロコが落ちたり、あるるの目は忙しいのぅ（笑）。で、計算のやり方は理解できたのかの？」

あるる「うっ・・・急にたんこぶが痛みだした・・・・イタタタタ」

博士「ふぉっふぉっふぉっ。相変わらず、わかりやすいのぅ（笑）」

あるる「てへ。公式は難しくってよくわかりませんでしたけれど、数字を出すにはいろんなことを考えなければならない・・・ってことはわかりました！！　そこは面白かったです」

博士「おお、そうか。今日のところはそれで良しとしよう。その『面白かった』気持ちを大切にするんじゃぞ」

あるる「はい。ありがとうございます！　よーし、いつの日か、博士のようにスラスラと難しい計算ができるようになるぞーーー！　おーっ！」

博士「あるるよ、そんなに前のめりになると、またぶつけるぞ」