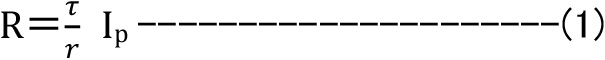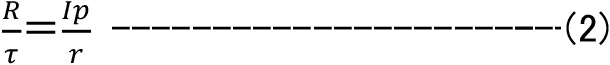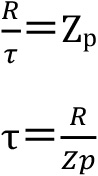♪♪ ちゃんちゃかちゃかちゃか〜・・・♪♪

あるる「えい、ほっ、よっ・・・」

博士「おはよう、あるる。ラジオ体操か？　朝から元気じゃのぅ」

あるる「おはようございます！　夏休み中、おじいちゃんと毎日やっていたので、習慣になってしまって。博士もどうです、ご一緒に」

博士「ラジオ体操か、懐かしいなぁ。よし、わしも加わるとしよう。ふん、はっ」

あるる「博士、なかなか機敏な動きじゃないですか」

博士「そうか。結構カラダは覚えているもんじゃのう。ほれ、いよっ」

♪♪腕を振ってカラダをねじります♪♪

博士「あるるよ、それでは全身を揺らしているだけじゃぞ。もっと下半身をしっかり大地につけて、ウエストをねじるのじゃ」

あるる「こうですか？」

博士「もっとじゃ。こうじゃ！」

あるる「急に鬼コーチか（笑）」

博士「“ねじり”は大事じゃからな。おおっ、そうじゃ！！！」

あるる「どうしたんですか、急に」

博士「“ねじり”といえば、「極断面係数」については、まだ話はしておらんかったな。よし、今日はそこからはじめるぞ！」

あるる「また難しそうな言葉が・・・は〜い、がんばりまぁ〜す」

前回の断面二次極モーメントに続いて、今回は極断面係数を説明します。

極断面係数は、断面二次極モーメントと同様に断面形状からその材料のねじれ強さを表すものです。

断面二次極モーメントは、ねじれ量を算出するときに、極断面係数は応力度を算出するときに使います。

言い換えると、ねじりモーメントに対して
断面二次極モーメントは、どれだけねじれにくいか
極断面係数は、ねじれにどれだけ耐えれるか
を表す数値で、両方とも材質には関係がなく断面形状の性能を表すものです。

まず、前号の式（10）

R：ねじり抵抗モーメント

T：ねじりモーメント（トルク）

τ：ねじり応力

I_p：断面二次極モーメント

ここで、I_pとrの関係で表されるのが、極断面係数Z_pです。

第87回で断面係数を説明しましたが、それを理解しているとわかりやすと思います。

式（2）(3)より

となります。

このτがねじり応力ですが、ねじり抵抗モーメント(R)を極断面係数(Z_p)で除した値であり、

極断面係数(Z_p)は、断面二次極モーメント(I_p)を半径(r)で除した値です。

つまり、断面二次極モーメントと同じく、材質には全く関係のない値です。

断面二次極モーメントの単位はmm⁴でしたが、
極断面係数はそれを長さで除しているので単位は、mm³となります。

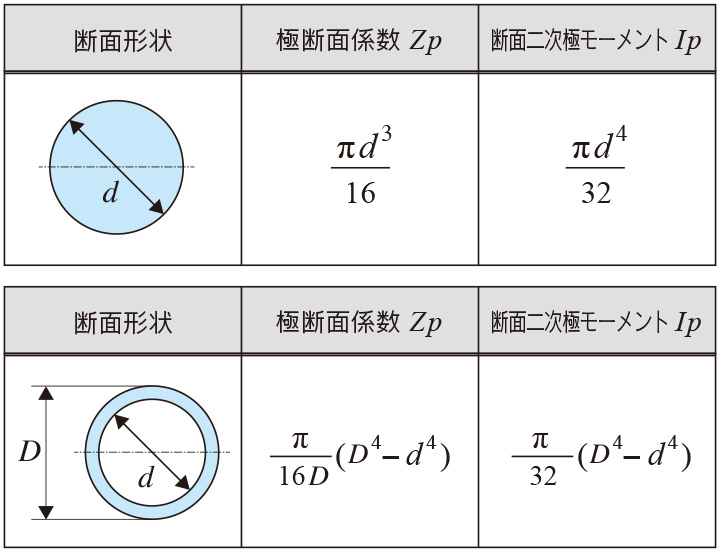
前回の式(2)で円形断面の断面二次極モーメントを示しました。

　I_p=πD⁴/32

極断面係数はこれをr(=D/2)で除したものなので

　Zp＝πD³/16

となります。

つまり中実軸の場合に、軸のねじれにくさ（ねじり剛性）は軸径の4乗に比例し、
軸の破壊しにくさ（ねじり強度）は軸径の3乗に比例するわけです。

このことから、ねじり剛性については中実軸より中空軸が軽量で有利なことがわかります。

中空軸は、外径の値から中空径の値を引いた値となるので、まとめると以下のようになります。

実は前回、今回で説明したねじりに関することは、円形断面に限られます。
（円形断面とは、中実円、中空円、中実楕円、中空楕円）

矩形断面などそれ以外の形状においては、弾性学となり、断面の湾曲のためそのせん断応力は辺の中央部で最大になり、4隅の角では、0となります。

イメージで言うと、ゴムの丸棒をねじると外周で応力が最大になりますが、長方形断面のゴムの角柱をねじると広い面の中央部（中心から一番近いところ）が最も湾曲することが想像できるかと思います。ここで応力が最大となるわけです。

さらに、開断面形状（H鋼やナット溝のあるアルミフレーム）ではまた異なった挙動となります。

これらについては改めて説明いたします。

博士「どうじゃ、あるる。わかったかの？」

あるる「う〜・・・今回も難しかった・・・。でも「ねじり」が大事なのはわかりました。しかも極断面系数は、素材に関係ないというのも驚きでした」

博士「そうじゃろう。深く知ると面白いことがたくさんあることが、わかってくるんじゃ。ゆっくり理解していこうな」

あるる「はいっ！！　それにしても、極断面係数って言いにくいですよね。えっと、きょく、きょくだん・・・、きょ、きょくだん・・めん・・・」

博士「おいおい、舌を噛むでないぞ」

あるる「＠♪×○□△・・・時すでに遅し・・・痛いです（泣）」