今月注目する基礎用語はコチラ！！
↓↓↓
今月の基礎用語：ゲ＃032
現場スケッチ

sketch on site

あるる「今年も咲きましたねぇ〜〜。桜、キレイですねぇ〜〜。春ですねぇ〜〜〜」

博士「今年は予想に反して開花が遅かったが、いやぁ、見事じゃのぅ」

あるる「そういえば、博士がとっても絵がお上手だと知ったのも、満開の桜の下でした。覚えてますか？」

博士「はて、そんなことがあったかのぅ」

あるる「ありゃ、忘れちゃったんですか？　それから道具を使わなくても寸法がわかる“スゴ技”を教えてもらったのも同じ時期でした。ほら、花壇の周りを歩いただけでサイズを測ってくれた・・・」

博士「（ポン！）おお、そんなこともあったのぅ。思い出したぞ、何年前かの？」

あるる「確か、2020年でしたから、4年前ですね」

博士「そうか、もう4年も経ったのか。懐かしいのぅ。ではその頃を思い出して、この桜並木の距離を一緒に測ってみようではないか」

あるる「はいっ！！！」

博士「わしの一歩はだいたい70センチじゃから・・・」

あるる「あああああっ！！」

博士「どうしたのじゃ？！　もう、びっくりさせおって（ドキドキ）」

あるる「博士ぇ、あるるは飛行専門なので、歩数では計れません！！」

博士「ふぉっふぉっふぉっ、そりゃそうじゃ。では、間違えないように一緒にカウントしておくれ」

あるる「はいっ！！！　お任せください！！！」

今回は「スケッチ」についてお話します。

スケッチといってもアイデアスケッチ、説明用の鳥瞰図などもありますが、今回は図面を書くために設置環境や機械装置の採寸を行う場合に関して、そのポイントを記します。

現場へ行って採寸する場合に、うまく測れない。
また帰ってきて図面化しようと思ったら、採寸漏れがあったなどで苦労した経験を持つ人も多いのではないでしょうか。

まず、フリーハンドのスケッチ図といっても図面です。
他の人が見てもわかるようにする必要があります。

基本的に「第三角法」で、図面と同じ規則で描きます。
出来れば必要な部分以外も描いておくと、他の人もイメージが掴みやすくなります。

問題は必要な寸法を漏れなく正確に測定し、解りやすく記入することです。

まず、計測漏れ防止ですが、X,Y,Z各座標における基準を決めることがポイントです。

「Z」は、通常フロア面ですが、段がついていることもあるので基準が必要です。

基準を意識すると、測った寸法が宙に浮いているという事がなくなります。

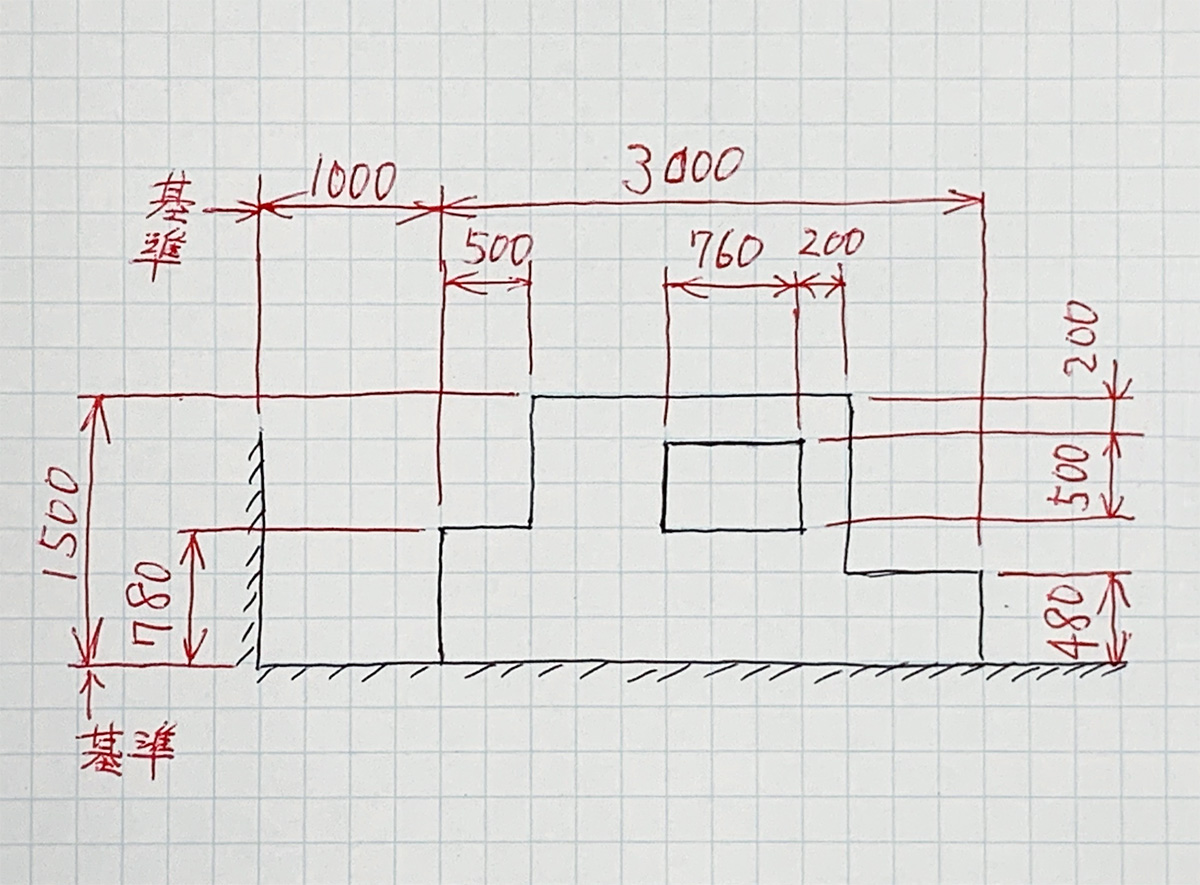
下図（Fig.1）の 760×500 の位置について、鉛直方向は基準は下面ですが、上面から下がってみることで位置を特定できます。

実際の図面では基準面から寸法記入すべきですが、現場スケッチでは測定困難な場合もあり、順にたどることが出来れば良いです。

しかし、水平方向において、枠は測定してありますが位置を特定できません。
基準から見れば、抜けている寸法がどこかがわかります。

Fig.1

正式には「コンベックスルール」と言います。

スケッチする際に当然必要なもので、巻き尺の中で、断面が湾曲した金属テープのものをさします。

先端の爪は固定爪と移動爪があり、固定爪は引っ掛け測定専用で、移動爪は引っ掛けでも突き当てでも使用できます。

また湾曲しているため、伸ばしてもある程度までは保持します。
これを利用して、手の届かないところの寸法を測ることが出来ます。

メモリのある凹面を内側にしてU字に折り、対象物に向けて伸ばします。
対象物に突き当てて、コ型に広げて目盛りを読みます。

・角度ですが、分度器がない場合は勾配で測ります。

・メンディングテープを持っていると便利です。

鉛筆やボールペンで書くことが出来て剥離性も良いので、端部ではない面でも貼って仮に基準線を引いておくこともできます。

・フロアに基準線を引きたい場合は、養生テープと油性ペンが良いです。

・手が届かない場所はレーザー測長器が便利ですが、無い場合は前記のようにコンベックスを伸ばします。

フリーハンドでは線種がわかりにくいため、色分けすることが有効です。

例えば

実態として存在するもの---黒
寸法線、寸法数値 ---------赤
移動時など特別な位置-----青

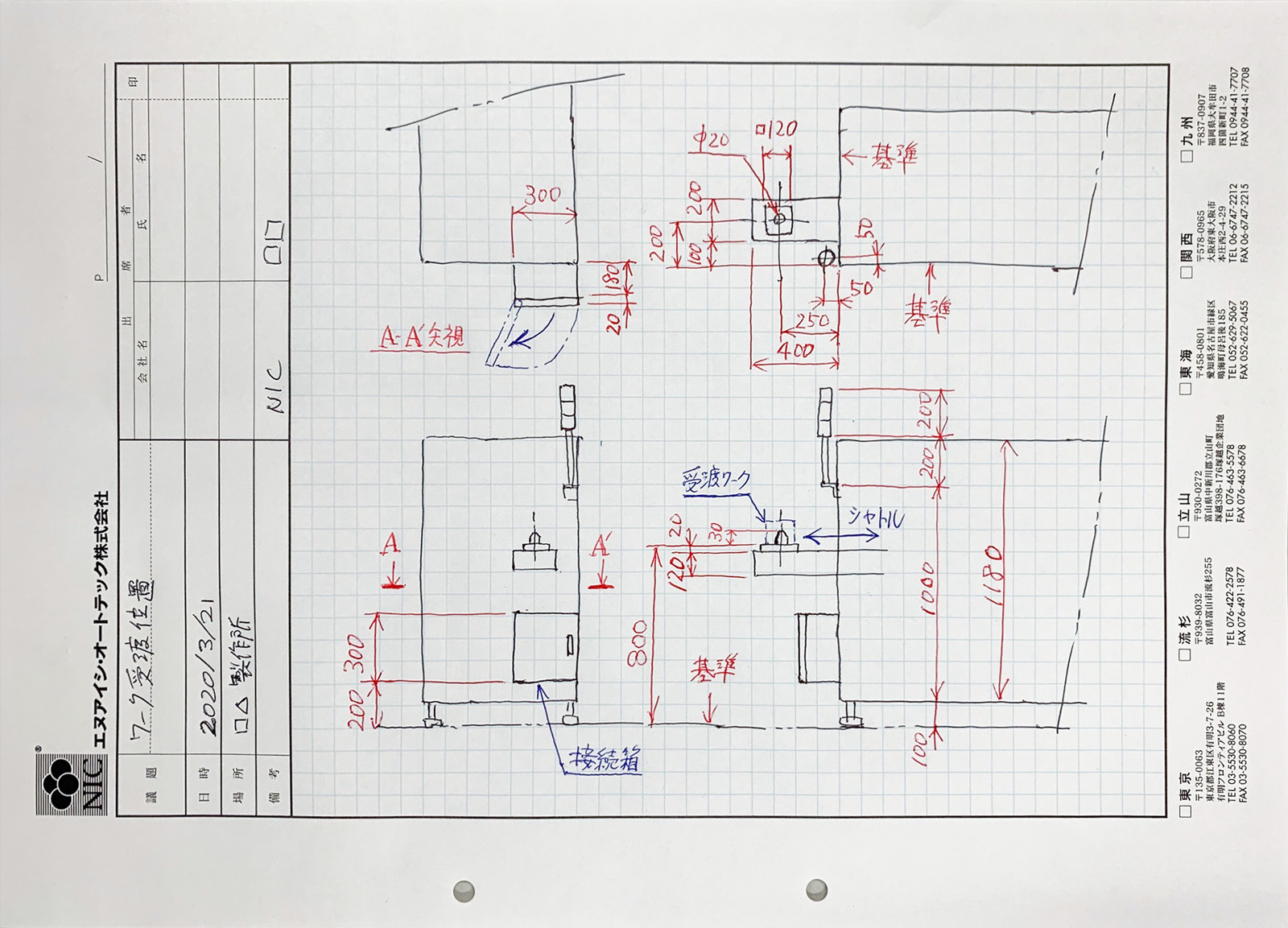
とすると、下図のようになります。

黒・赤・青を用いたスケッチ

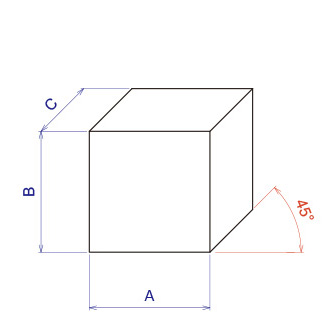
対象物がシンプルであれば、立体図で表した方がわかりやすいです。
立体図には、「斜投影図」と「等角投影図が」あります。

斜投影図は、正面図としてA,B寸法を実際の比率で描き、奥行き線は45°として実際の比率の1/2で描きます。

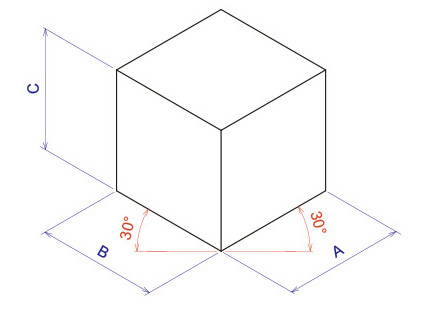
等角投影図は、基準線に対し左右30°の線と垂直の線を引き、これを基準として平行に線を描いていきます。

寸法はA,B,Cすべての方向で実際と同じ比率で描きます。
フリーハンドでも、これらのポイントを押さえれば見やすいものが描けます。

近年はレーザー測長器のみならず、3Dスキャナーまで便利な機器がありますが、あえて泥臭く、特別な機器（コンベックス以外）を持ち歩いていない場合でも、とりあえずの把握が出来る方法を説明します。

寸法はコンベックスやレーザー測長器など、一般に携行出来るもので充分計測できますが、荷重を測りたい場合、荷重計などはなかなか持ち歩かないと思います。

そのような場合、正確性には欠けますが、とりあえず把握する方法として、自分の身体を利用することが出来ます。

まず「指」で台秤等を押してみてその力を把握しておきます。

親指--100N、人差し指--45N、薬指--30N、小指--20N など、あくまで適度な痛みを感じる安全な範囲で、怪我のリスクのない範囲としてください。

もちろん機構部など危険性のある個所については、この方法を使ってはいけません。
操作レバーやハンドルの動作力など、本来の使い方で手を添えるところに関しては、このような方法で大体の荷重を把握することが出来ます。

次は「足」を使った計測です。

装置の搬入経路などの概要を把握するために、自分の通常の歩幅を把握しておくと便利です。
地図アプリなどで、あらかじめわかっている道のりで歩数をカウントしてみます。

200ｍが278歩であったなら、
200÷278≒0.72ｍ

これさえわかっていれば、通路の幅はコンベックスで測るとして、歩きながらカウント。

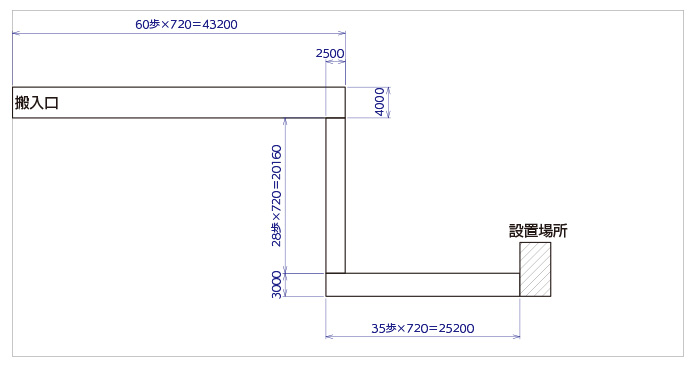
幅4ｍを60歩、右に曲がって幅2.5ｍを28歩、左に曲がって幅3ｍを35歩　

そして歩数から距離を算出して、伝えることが出来ます。

また、「目」を使って、柱のスパン数をカウントすることも有効です。

ちなみに歩行と言えば、時間軸を加えると下記のような場合に使えます。

電車の車両の長さは、JR在来線や大部分の私鉄においては20ｍ（一部例外あり）、新幹線では25ｍ（ミニ新幹線は20～23ｍ）です。

新幹線ホームのエスカレーターを上がったら6号車、自分が乗るのは12号車であれば
25ｍ×6両＝150ｍ

普通の歩行、時速3.6kmで１ｍ/secなので
150秒＝2.5分
発車時刻まで3分あれば、普通に歩いて大丈夫という事になります。

距離測定に関し、歩いていくことが出来ない場合には、スケールが1枚あれば測量の理屈を応用して算出することが出来ます。スケールはプラスチックスの透明の物が良いです。

まず、両眼視差での距離測定です。

人の左右の目のピッチ(P)に対して、腕を伸ばした時の長さ(Q)は約10倍と言われています。

P＝65mmとして、例を示します。
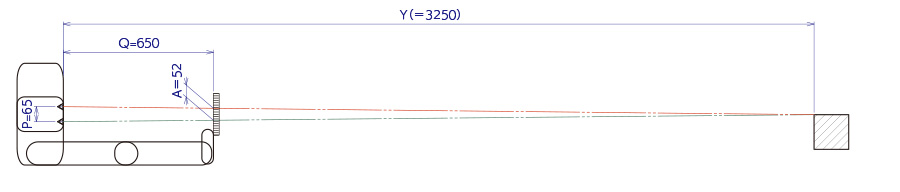
スケールを持った腕を伸ばして読み取ります。

Fig.2
右目で対象物の一点を見てスケールの目盛りを読みます。
左目で対象物の一点を見てスケールの目盛りを読みます。

この差をAとします。対象物までの距離Yは
Y＝(P×Q)/(P－A)
＝(65×650)/(65－52)
＝3250
となります。

P、Qは実際固定値ですから、Aを読んで簡単な算出で導き出すことが出来ます。

Fig.2

但し、この方法は極めて短距離でしか使えません。
５ｍ以上だと差が小さくなってしまうからです。参考に1ｍごとのA寸法を出しておきます。

参考

対象物の寸法がわかっている場合で両眼視差を使う場合

この方法では、かなりの遠距離にも適合します。

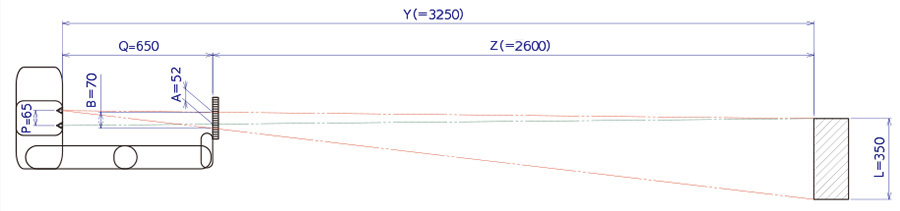
左目で対象物の両端を見てスケールの目盛りを読み、その差をAとします。

右目で対象物の片側端を見てスケールの目盛りを読み、左右の視差寸法をBとします。
このAとBの比がスケールから対象物までの寸法に比例します。

スケールから対象物までの距離Zは

Z＝(A/B)×L×(Q/P)
＝(52/70)×350×(650/65)
＝2600
となります。

Fig.3

遠方でも簡単に認識できる目標物として乗用車（約４ｍ）、両開きの窓や扉（約1.8ｍ）などがあります。

そして腕を伸ばした位置を基準としたZ寸法で考えると、非常に簡単な計算で距離が求まります。

条件として両眼のピッチと腕のリーチの比を1:10として固定すると

Z＝(A/B)×L×10

という簡単な式になります。

またA、Bは

A＝P×Z/Y
B＝L×Q/Y

となります。例としてL＝4000ｍｍで10ｍごとに計算してみると
以下となり、Z寸法がL寸法を10倍にし、A/Bを乗じた値になります。

対象物の寸法がわかっている場合は、両眼視差を使わなくても簡単に距離を求めることが出来ます。

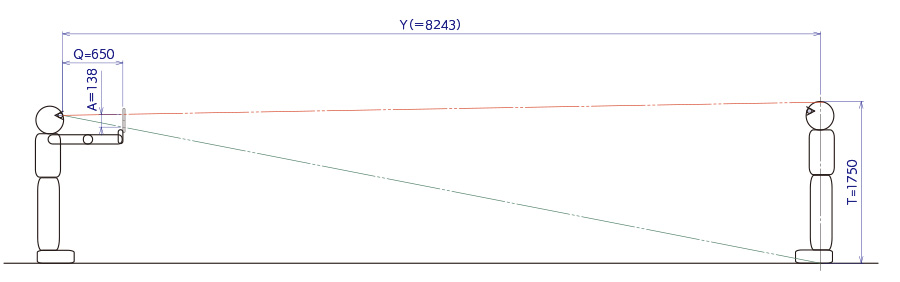
対象物の両端を見てスケールの目盛りを読み、その差をAとします。

対象物までの距離Yは
Y＝(Q×T)/A
＝(650×1750)/138
≒8243

Fig.4

色々な測定器が発達して便利になっていますが、自分の身体と普段カバンの中に常備しているもので、出来ることを知っておくと意外な時に役立ちます。

あるる「スケッチの方法って、本当にいろいろあるんですねぇ〜」

博士「面白いじゃろう。今便利な道具がいろいろあるが、昔はそんなものはなかったから、わしも若い時はいろいろと工夫したもんじゃ」

あるる「だから博士は今でも、こんなに絵が上手いんですね。やっぱり自分のカラダを道具にできたら最強ですよね！」

博士「おお、スケッチの真髄がわかってきたようじゃのぅ」

あるる「あっ！　クレープの台発見！！　しかもいい匂いです！」

博士「相変わらずめざといのぅ。本当じゃ。ここまで甘い匂いが漂ってきておる」

あるる「ならば早速調査をせねば！　では博士、あるるはこれからひとっ走り、あの屋台との距離を測りに行って参ります！　では後ほど！！（シュタッ！）」

博士「早いのぅ、もう見えなくなった・・・クレープの威力はすごいのぅ・・・」