いまさら聞けない基礎用語【コ】#038 固有振動数
公開日時:2024/10/30
みなさん、こんにちは。基礎用語、案内役のあるるです。
今回注目する基礎用語は、コチラ!
↓↓↓
今月の基礎用語:コ #038
固定振動数
natural frequency
博士「あるるよ、今日は面白いものを見せてしんぜよう」
あるる「え?なんですかー?(ワクワク)」
博士「ほれ!!」
あるる「わー、振り子、ですか?」
博士「さよう。研究室を整理しておったら、この振り子の模型が出てきてな。懐かしくて思わず磨いてしまったわい(笑)」
あるる「どうりでピカピカしてますね。動かしていいですか?」
博士「もろんじゃとも」
あるる「カッチカッチカッチ・・・面白いですよねぇ〜、この振り子の動き。ずっと見てられます〜〜」
博士「“ニュートンのゆりかご”とも呼ばれておるぞ」
あるる「ゆりかごですか〜。カッチカッチカッ・・・ふぁ〜〜〜〜。あれ?なんだか眠くなってきたような・・・」
博士「(そっと耳元で)あなたはだんだん眠くな〜る、ねむくな〜〜る〜〜(笑)」
あるる「博士ぇ〜、やめてください。これじゃ催眠術ですよぉ〜〜〜」
自由振動
「固有振動数」というと、共振を避けるために重要であるとか、剛性のためには高い方が良いなどは既知の方が多いと思いますが、あらためて考えてみましょう。
はじめに「振動とは何か」、「第69回振動に関して」の冒頭に記しましたが、振動とは、平衡な点を中心として周期的な運動を繰り返す状態です。
振動には以下の要素があります。
振動数(周波数):1秒間の往復回数
振幅(変位):往復している幅
速度
加速度
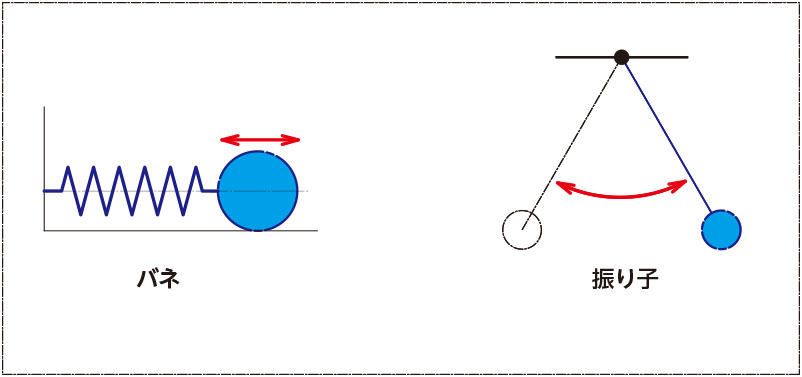
下図のようなバネや振り子は往復運動をします。
最初に与えた条件以外に外力が加わらない状態で起こる往復運動を「自由振動」と言います。
自由振動
単振動
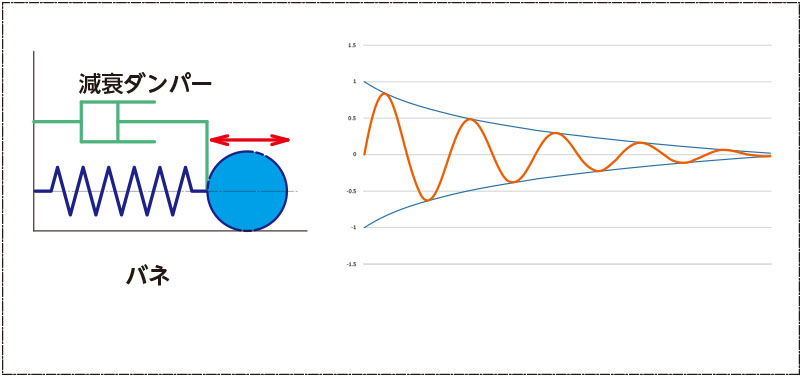
減衰自由振動
強制振動
それらに対し、継続的に外力が加わる場合は「強制振動」と言います。
ブランコで最初に後退した位置から足を浮かせ、そのあとは動かずに揺れに任せるのが自由振動で、漕ぎ続けるのが強制振動です。
自由振動と強制振動
固有振動数
固有振動数とは、対象物が自由振動を行うときの単位時間に起こる往復運動の回数で、1秒間に10往復であれば、固有振動数は10Hzとなります。
バネや振り子の自由振動を考えるとわかりやすく、最初に与える条件(離す位置、振れ幅)に関わらず、1往復の時間は同じであり、つまり振動数は変わらないという事になります。
これが固有振動数です。
すべての物体は固有振動数を持っており、固有振動数は外部に減衰力があると変化します。
また、固有振動数は質量と剛性によって決まるものであり、先述した自由振動のモデル図で言うと、バネが剛性で球体が質量です。
固有振動数は質量が大きくなるほど低くなり、剛性が高くなるほど高くなります。
陶器のカップを棒で叩くと音が響きますが、この音の周波数が固有振動数となります。
空中に紐でぶら下がった状態と、テーブルに置いた状態では音の高さが変わります。
テーブル上の方が低い音となり振動数が下がるのですが、これはテーブルに接することで減衰効果が発生したわけです。
また、手で軽く持つのと、しっかり握った場合でも同様に音の変化があります。しっかり握った場合は減衰力と剛性がともに上がったわけです。
つまり、固有振動数を正確に実測することはなかなか難しいのです。
装置架台などを構造解析で求めても、実際には設置した床条件で変わってしまいます。固有振動数が重要である最も大きな理由は、共振を避けて破損や機能障害を防ぐという事でしょう。
共振とはブランコの例で言うと、漕ぎ手がブランコの固有振動数に合わせて漕ぐと振幅はどんどん大きくなりますが、合わせない場合、振幅は収束します。つまり、建物や機械装置において外力の振動数と固有振動数が一致すると大きな振幅になり、破壊を招きます。
回転機構についても同様の事が言え、回転軸の固有振動数と回転数が一致すると大きな振動が起こります。回転機器の停止時に回転数が下がっていく過程で一瞬、ブルブル震えるポイントがあることで理解できると思います。
固有振動数と剛性
次に剛性です。
固有振動数は質量と剛性によって導かれるものなので、もちろん関係性は深いのですが、ロボット架台のようにフロア面を拘束として考えると、振動数には重心位置も大きく関係するので、固有振動数と剛性にある程度の相関はあるものの比例するとは言えません。
もちろん、床の種類によってもその接触部分の硬さや摩擦により振動は変化します。
重心高さについて言うと、メトロノームを考えるとわかりやすいのですが、錘(おもり)が上にあるほどゆっくり揺れます。振動数が下がるという事です。
また、同等の剛性でありながら軽量であると固有振動数は高くなります。これをロボット架台などで考えると、架台内部の下ベースに機器を積載して全体の重心位置が低くなると全体の振動数は高くなります。架台上部にユニットを取りつけて重心位置が高くなると振動数は低くなります。
しかしながら、どちらの場合においても、ロボットが動作した場合の反力でかかる荷重による変位量は同じで、全体の振動数が異なっても架台の剛性は変わりません。
ロボットの往復動作は高速でもせいぜい3Hz程度であり、通常の装置架台の固有振動数(20~70Hz程度)とは大きな差があるため、共振により振幅が大きくなることは考える必要はないです。
ですから、固有振動数で評価する場合は剛性に関与する構造体のみで考えれば良いです。
全体の質量や重心位置などの条件が同じであれば、固有振動数と剛性は相関関係となります。
では、全体の系の振動数が機能上全く関係ないかというと、そうではなく、ロボットの急加減速、停止においてはもっと周波数の高い成分が出ることが考えられ、停止後の減衰時間をより短くするためには出来るだけ全体の系の振動数を高めておくことが有効であろうと考えられます。
高速のロボットで高精度の仕事を確実に実行するために、剛性が高く、かつ固有振動数も高い架台はまさに縁の下の力持ちの役割を果たします。
あるる「さっきは思わず催眠術にかかっちゃうところでしたけど、やっぱり振動って面白いですよね」
博士「ふぉっふぉっふぉっ、ちゃんと目覚めてくれてよかったわい(笑)」
あるる「自由振動に強制振動。そしてすべてのものが固有の振動数を持っている!」
博士「きちんとポイントを押さえられたのぅ。えらいぞ、あるる」
あるる「はいっ! ありがとうございます!」
あるる「じゃ、そろそろ博士、行きますか?」
博士「おや、どこにいくのじゃ?」
あるる「ブランコですよ! さきほどの博士の説明を聞いて、急にブランコに乗りたくなりました。久しぶりに思いっきり漕ぎましょう!」
博士「よし! 気分転換に振り子気分を味わおうぞ!!」