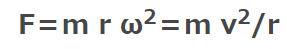みなさん、こんにちは。基礎用語、案内役のあるるです。

今回注目する基礎用語は、コチラ！
↓↓↓
今月の基礎用語：エ　＃008
遠心力　Centrifugal force

あるる「えい、えいっ！　やったー、回ったー＼(^o^)／」

博士「楽しそうじゃな、あるる。何を・・・おお、コマではないか。懐かしいのぅ〜」

あるる「はいっ！　昨日、おじいちゃんに教えてもらいました。なかなか上手に回せなかったんですが、一晩特訓して、ほら、この通り！」

博士「よく回っておる。すごいぞ、あるる。一晩で習得したのか。（その情熱を学問にも少し活かしてくれたらのぅ・・・）」

あるる「え？　何か言いましたか？」

博士「いや、何も・・・。ところであるる、そのコマは、何で回っているかわかるかの？」

あるる「ん？　勢い？」

博士「ある意味正解じゃが、その勢いのみなもとは遠心力じゃ。覚えておるか？」

あるる「あっ！　博士がバケツをブンブン振り回した、あの遠心力、ですか？」

博士「その通り。あるるのことじゃから、そこしか覚えておらんのじゃろう（笑）」

あるる「お、お見通しで・・・」

博士「ふぉっふぉっふぉっ。では良い機会じゃ。しかと復習しようでははないか」

【今月のまめ知識 第74回】人工衛星についての回では、「第一宇宙速度」のお話をしましたが、第二、第三宇宙速度もあります。ちょっと整理してみましょう。

「第一宇宙速度」は、地表近くを落下せずに円軌道で周回し地球の衛星となるための初速度で、約7.9km/secでした。

「第二宇宙速度」は、地球の引力圏を脱出する速度です。第一宇宙速度からさらに速度を上げていくと、楕円軌道となってその遠地点が大きく成っていき無限大となると軌道は放物線となります。

つまり地球の引力圏を脱出するわけで、この時の初速は約11.2km/secです。ただし、この場合にその物体は、太陽の引力圏で楕円軌道を描き人工惑星となります。

「第三宇宙速度」は太陽の引力圏からも脱出する速度で、約16.7km/secです。

これらに関して詳しくは物理の教科書または一般のweb上で多く説明されていますので、あえてこれ以上は深く入りません。

引力圏から脱出するということは、簡単に言うと、糸に重りを付けて振り回し、どんどん速くしていったら糸が切れて重りが飛んで行ったという事です。

普通は「遠心力で糸が切れた」という人が多いのではと思います。

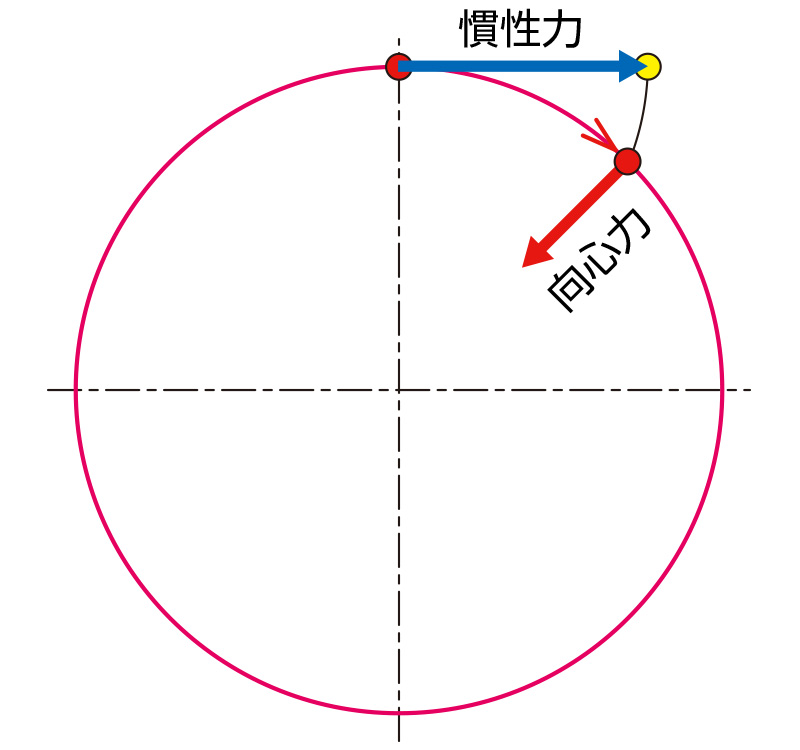
物理的に表現すると、「慣性でまっすぐ運動しようとしている重りを、向心力（糸の張力）で強制的に一定の円軌道に進路を変えているが、速度が速くなる事で慣性力が大きくなり、この円軌道を保つための向心力が糸の張力を越えた」ということになるのですが・・・

「遠心力」というのは、当たり前のようでいて、実はわかりにくい力なのです。

我々は、遊園地の回転遊具でも自動車でカーブする場合でも外側へ引っ張られる力を感じ、遠心力と言っています。
しかし、中心から遠ざける力が積極的にかかっているわけではありません。向心力に対応する反力なのです。

別の言い方をすると、自動車で直進していて急ハンドルを切ると、慣性で質量のある物体はそれまでの運動を続けようとします。

しかし、タイヤの向きが変わることで、タイヤは向心力を発生させて自動車の運動方向を変えます。下図のようにこれを外から見ると良くわかります。

ですから、スリップして飛び出すのは遠心力ではなく、慣性力なのです。

慣性力と向心力の方向

ハンマー投げも同様で、手を離した後はその瞬間の接線方向へまっすぐ飛んでいきます。

もし、積極的な力としての遠心力が存在するなら、この接線よりも外側へ運動することもあるはずですが、そんなことはあり得ません。

しかしながら、機械屋さん的に考えると、荷重に対する応力のように反力も認めなくてはいけません。ここで必要になるのがどの座標系で見ているかです。

外部から慣性座標系として見ると、上述のように「遠心力など存在しない、それは慣性力である」という事になります。

一方、運動体の内部（自動車に乗っている立場）から回転座標系として見ると、「外側から引っ張られる力＝遠心力」としてとらえることができます。

どちらにしてもこの外向きに発生する力は向心力の反力であるため、それに等しい大きさで

であり、

言葉の違いで同じではないかという事になりますが、実際に積極的にかかっている力なのか、見かけの力なのかを理解しておく必要があります。

垂直多関節ロボットやスカラロボットなど極座標系のロボットでは、直線補間をしないで円弧動作をさせた場合には、把持しているワークに遠心力が掛かります。

また、進行方向に対しては慣性力が掛かりますから、それが組み合わさってかかることになります。

そこで、直線動作、円弧動作それぞれの場合の”力のかかり方”を考えてみたいと思います。

モデルとして、アーム半径500㎜で500㎜の距離を0.5秒で動作するロボットで
把持ワークの質量を0.2kgとして、慣性力、遠心力を算出してみます。

計算式を理解する上で、プロセスが大切なので、ここから先は直接ブログ記事をご参照ください♫

↓↓↓↓↓↓

【今月のまめ知識 第76回】　ロボット動作時の把持ワークに掛かる荷重

https://alfaframe.com/mame/20537.html

あるる「こんな感じでまとめてみましたが、いかがでしたか？」

博士「おお、よく頑張ったではないか（モグモグ）。えらいぞ、あるる（モグモグ）」

あるる「あ、博士、何か食べてますね⁈ 」

博士「おや、バレてしまったか。久しぶりにコマを見たら、駄菓子が食べたくなってのう。ホレ、あるるの分もあるぞ。好きなモノをたくさん食べなさい。頑張ったご褒美じゃ」

あるる「やったー！！　わーい、わーい＼(^o^)／　まずは麩菓子から、いっただきまーす！！！」

あるる「博士ぇ、遠心力って、美味しいですね♫　次はソース味にしよー♫（モグモグ）」

博士「うーむ、そうきたか、、、。あるるがもろもろの計算方法を理解するには、まだまだ時間がかかりそうじゃのう。まぁ、のんびり成長を見守るコトにしようかのぅ」