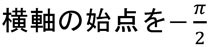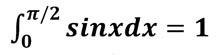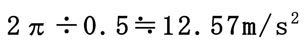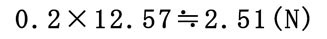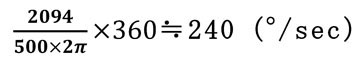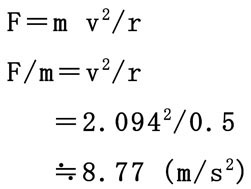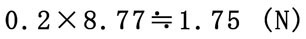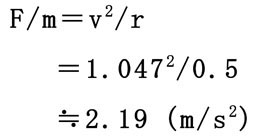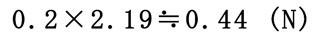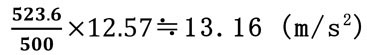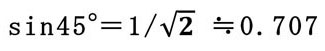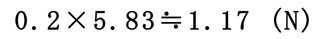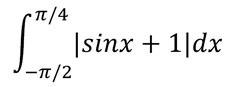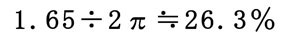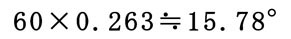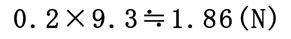【今月のまめ知識 第76回】 ロボット動作時の把持ワークに掛かる荷重
公開日時:2019/07/31
とあるのんきな朝のひと時
あるる「博士ぇ〜、最近のロボットってスゴいんですね!」
博士「おはようあるる。何はさておき、朝は挨拶からじゃぞ」
あるる「あ、ごめんなさい。博士、おはようございます」
博士「おはよう。で、ロボットがどうしたんじゃ?」
あるる「もう、すごいんですよ、ロボット! しかも大学生たちが作るロボットが
めちゃめちゃすごいんです\(^o^)/」
博士「大学対抗のロボットコンテストのことかの?」
あるる「そうそう、それです! おじいちゃんと一緒に見ていて、もう応援しまくりですよ」
博士「おお、それならわしも見たぞ。今年はドラマがあったのぅ」
あるる「ロボットって、いろんな要素がバランス良く作用しないと、うまく動かないんですね。
奥が深いなぁ〜」
博士「そうなんじゃよ!いいところに気がついたの、偉いぞ、あるる。ロボットの性能はもとより、
ロボットがどういう動きをするかを研究することが大事なんじゃぞ」
あるる「なるほど〜、奥が深いんですね・・・」
博士「ところであるるよ、前回話した「遠心力」は覚えているかの?」
あるる「もちろんです。さすがにそんなに忘れっぽくはありませんよ」
博士「その遠心力とロボットの動き、実に深い関係があるんじゃ。知りたいか?知りたいじゃろ?」
あるる「もちろんですっ!ぜひ、ぜひっ!」
博士「そ、そうか? では早速・・・(今日はやけに積極的じゃのう・・・)」
前回は「遠心力」に関してお話ししました。
垂直多関節ロボットやスカラロボットなど極座標系のロボットでは、直線補間をしないで円弧動作をさせた場合には
把持しているワークに遠心力が掛かります。
また、進行方向に対しては慣性力が掛かりますから、それが組み合わさってかかることになります。
今回は直線動作、円弧動作それぞれの場合の”力のかかり方”を考えてみます。
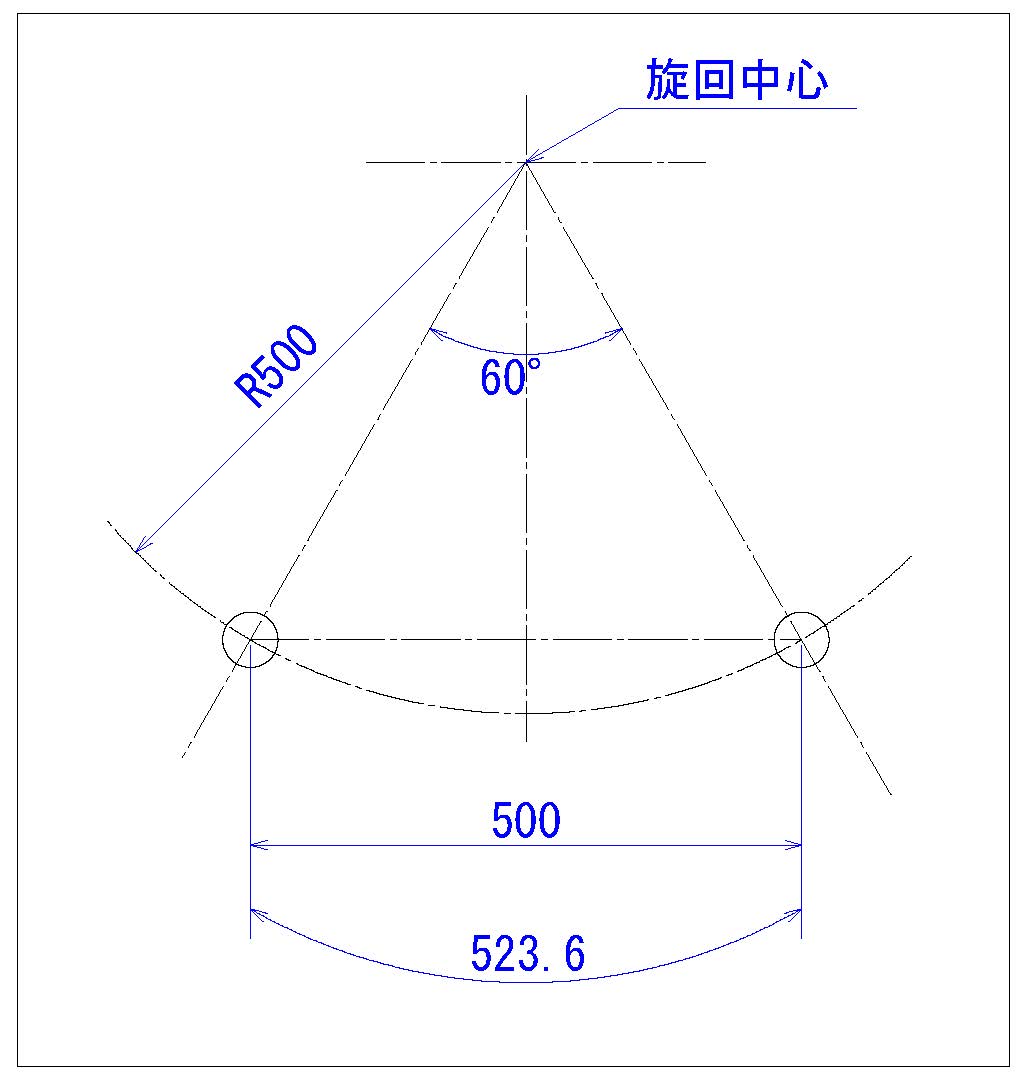
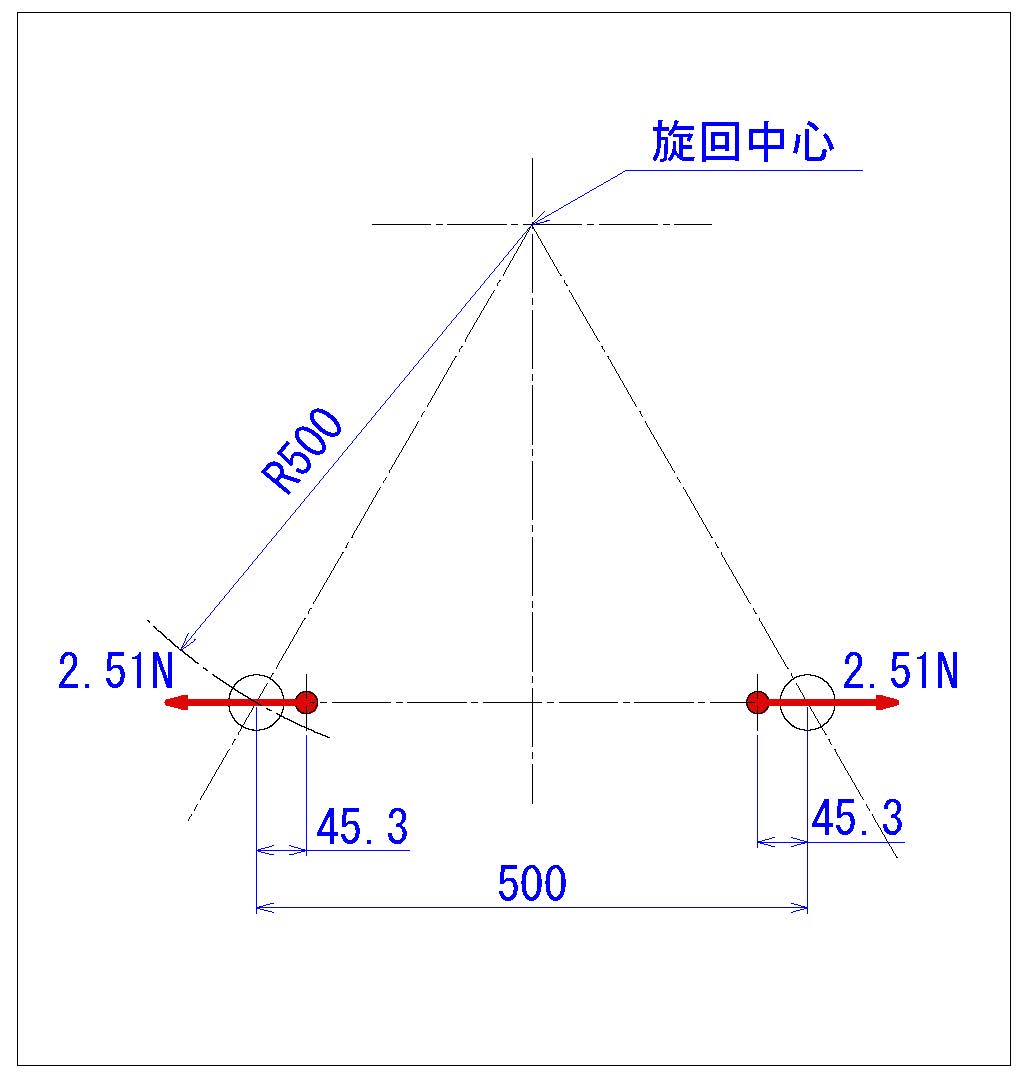
モデルとして、アーム半径500㎜で500㎜の距離を0.5秒で動作するロボットで
把持ワークの質量を0.2kgとして、慣性力、遠心力を算出してみます。
ここで移動距離ですが、これでちょうど500mmとなります。
----------------------------------------------------------------------------------
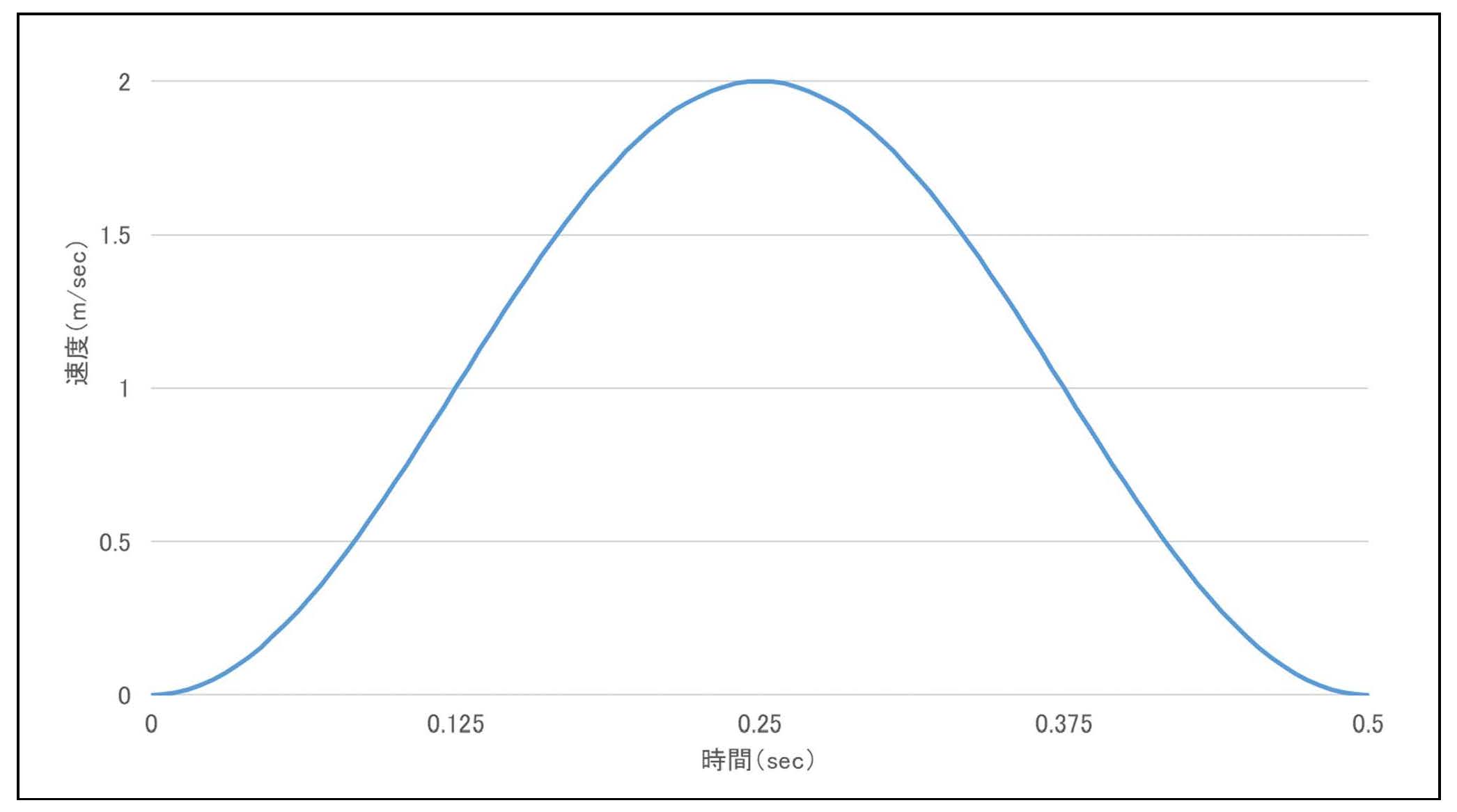
上記の波形は通常のsinカーブに対して
これを解くと2πとなり、縦軸振れ幅で2m/sec、横軸は2πを0.5secとしてスケールに合わせて換算すると0.5mとなります。
または正弦波の定積分公式を利用して図形的な解釈も可能です。
グラフ-2
----------------------------------------------------------------------------------
1. 直線動作の場合
と、算出されます。
つまり、直線補間した場合には
0.125secの位置で12.57m/s2、
0.375secの位置で-12.57m/s2
の加速度が掛かっていることになります。
そしてこの発生位置は
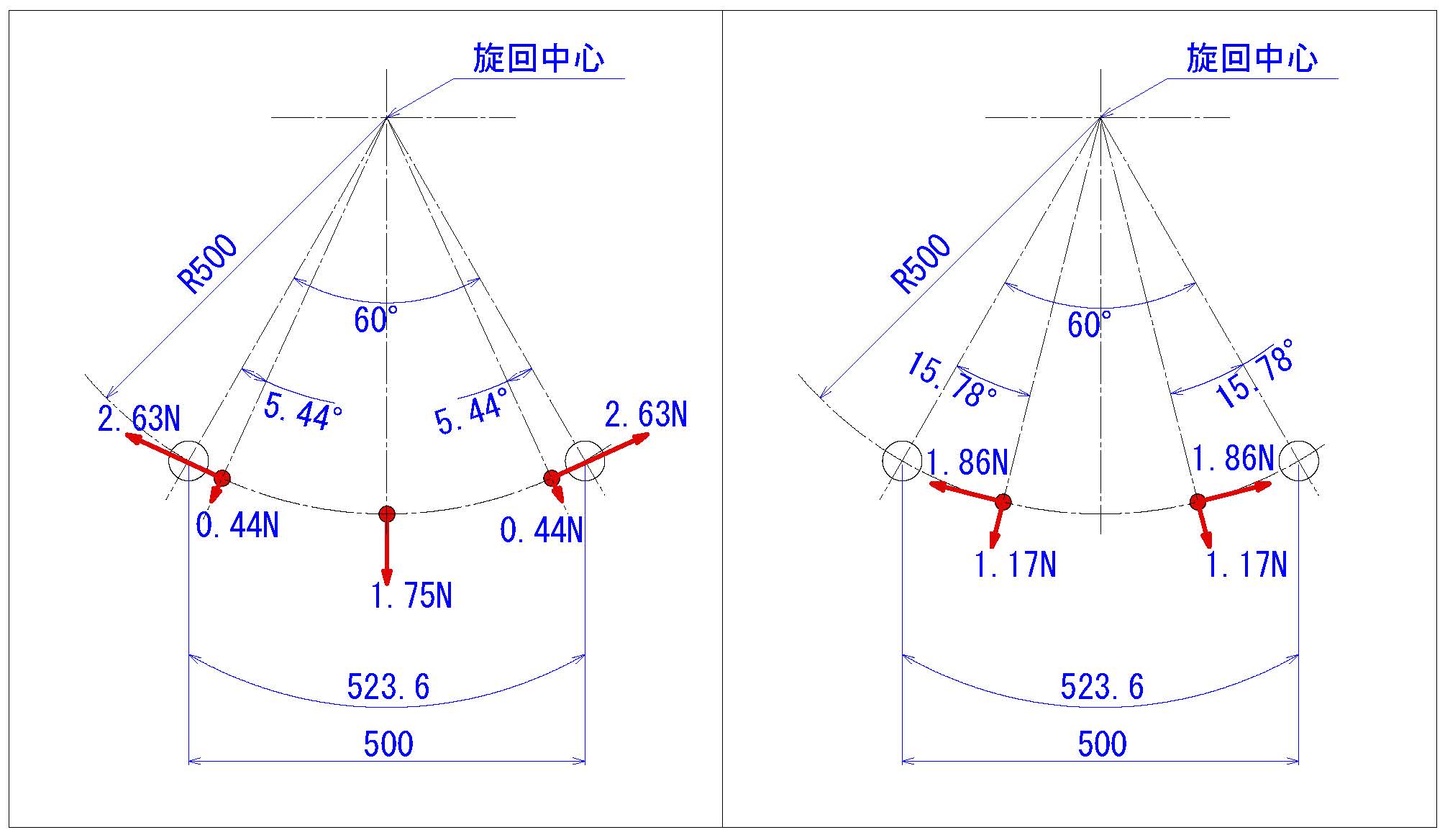
2.円弧動作の場合
③ 中間位置
これに加えてもう1点、慣性力と遠心力の両方がある程度掛かっている点として、ストロークの3/8の位置(0.1875sec)も算出してみましょう。
この位置は通常の正弦波形でX軸がπ/4(45°)の位置であり
直線動作の場合は、円弧動作に比べて遠心力が発生しないことに加え、進行方向の慣性力も少し小さくなっています。
しかし、垂直多関節ロボットの場合、直線動作ではJ2軸が動作するため、ロボットの前後方向に掛かるモーメントが大きくなり、架台に負担を与えることになります。
博士「どうじゃ、あるる。ロボットと遠心力の関係は、腑に落ちたかの?」
あるる「う〜ん・・・計算式は難しすぎて、なにがなにやらさっぱり・・・でも、〝力のかかり方が大事〟いうことだけはわかりました!」
博士「そうじゃな、あるるにはちょっと難しすぎたかの〜。計算はおいおい覚えておけばよい。今は大事なことが大事だということがわかれば良しじゃ」
あるる「あー、なんか、数字をいっぱい見たらお腹が空いちゃいましたよ。今日は「早お昼」にしましょうよ〜」
博士「数字を見ただけでお腹が空くとは! あるるらしいというか、先が思いやられるというか・・・」
あるる「博士ぇ〜、早く〜。お弁当買いに行きますよ!」
博士「この行動力が、学びに結びつけば言うことなしなんじゃが・・・」