あるる「・・・・・？　・・・！　・・・？？」

博士「おや、あるる。今日もスケッチに精を出しておるな。えらいぞ」

あるる「あ、博士。絵を描くって楽しいですね〜。おじいちゃんにも上手いって褒められちゃいました♪　

　ふふんふん〜♪」

博士「（さすがあるるのおじいちゃん、おだてるのが上手いのぅ笑）←心の声　

　今日は花壇を描いているのか。お花が綺麗じゃのう」

あるる「ありがとうございます！　ただ・・・」

博士「ただ？」

あるる「なんだか全体のバランスがうまく取れなくて・・・」

博士「どれどれ？　おお、それは花壇が小さすぎるのじゃ。どうみても横幅は3メートルはあるじゃろうて」

あるる「え？　そんなにありますか？」

博士「どれ、測ってきてしんぜよう。ちょっと待っておれ」

あるる「ありがとうございます！　さすが博士、いつも巻尺を持ち歩いているんですねー」

博士　（トコトコトコ・・・）

あるる「・・・って、博士！　歩いているだけじゃないですか！　もう〜」

博士「（にやっ）やはり、3メートルと30センチくらいじゃな」

あるる「え？！　なんでわかるんですか？　歩いただけですよね？　全然測ってませんよね？？」

博士「ふぉっふぉっふぉ。それでもわしにはわかるんじゃ（にやにや）。知りたいかの（にやにや）？」

あるる「はいっ！　ぜひっ！　もう、なんでも教えてください！！」

前回は現場スケッチに関してお話しましたが、その延長線です。

近年はレーザー測長器のみならず、3Dスキャナーまで便利な機器がありますが、あえて泥臭く
特別な機器（コンベックス以外）を持ち歩いていない場合でも、とりあえずの把握が出来る方法を説明します。

寸法はコンベックスやレーザー測長器など、一般に携行出来るもので充分計測できますが、荷重を測りたい場合、荷重計などはなかなか持ち歩かないと思います。

そのような場合、正確性には欠けますが、とりあえず把握する方法として、自分の身体を利用することが出来ます。

まず「指」で台秤等を押してみてその力を把握しておきます。

親指--100N、人差し指--45N、薬指--30N、小指--20N など、

あくまで適度な痛みを感じる安全な範囲で、怪我のリスクのない範囲としてください。

もちろん機構部など危険性のある個所についてはこの方法を使ってはいけません。

操作レバーやハンドルの動作力など、本来の使い方で手を添えるところに関しては、このような方法で大体の荷重を把握することが出来ます。

次は「足」を使った計測です。

装置の搬入経路などの概要を把握するために、自分の通常の歩幅を把握しておくと便利です。
地図アプリなどであらかじめわかっている道のりで歩数をカウントしてみます。

200ｍが278歩であったなら、
200÷278≒0.72ｍ

これさえわかっていれば、通路の幅はコンベックスで測るとして、歩きながらカウント。

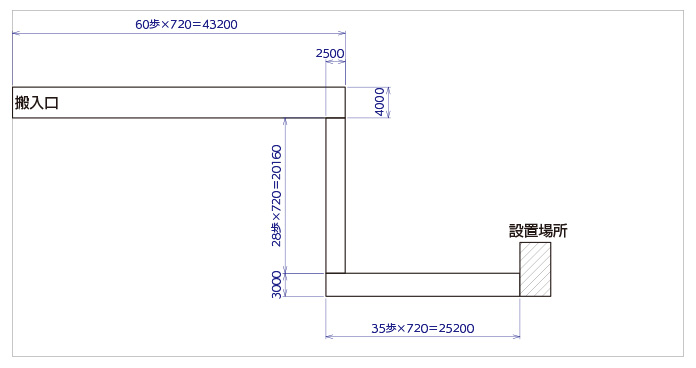
幅4ｍを60歩、右に曲がって幅2.5ｍを28歩、左に曲がって幅3ｍを35歩

そして歩数から距離を算出して、伝えることが出来ます。

また、「目」を使って柱のスパン数をカウントすることも有効です。

Fig.1

ちなみに歩行と言えば、時間軸を加えると下記のような場合に使えます。

電車の車両の長さは、JR在来線や大部分の私鉄においては20ｍ（一部例外あり）、

新幹線では25ｍ（ミニ新幹線は20～23ｍ）です。

新幹線ホームのエスカレーターを上がったら6号車、自分が乗るのは12号車であれば

25ｍ×6両＝150ｍ

普通の歩行、時速3.6kmで１ｍ/secなので
150秒＝2.5分

発車時刻まで3分あれば、普通に歩いて大丈夫という事になります。

距離測定に関し、歩いていくことが出来ない場合には、スケールが1枚あれば測量の理屈を応用して算出することが出来ます。スケールはプラスチックスの透明の物が良いです。

まず、両眼視差での距離測定です。

人の左右の目のピッチ(P)に対して腕を伸ばした時の長さ(Q)は約10倍と言われています。

P＝65mmとして、例を示します。スケールを持った腕を伸ばして読み取ります。

Fig.2
右目で対象物の一点を見てスケールの目盛りを読みます。
左目で対象物の一点を見てスケールの目盛りを読みます。
この差をAとします。対象物までの距離Yは

Y＝(P×Q)/(P－A)
  ＝(65×650)/(65－52)
  ＝3250

となります。

P,Qは実際固定値ですからAを読んで簡単な算出で導き出すことが出来ます。

Fig.2

但し、この方法は極めて短距離でしか使えません。

５ｍ以上だと差が小さくなってしまうからです。参考に1ｍごとのA寸法を出しておきます。

Fig.3
対象物の寸法がわかっている場合で両眼視差を使う場合

この方法では、かなりの遠距離にも適合します。

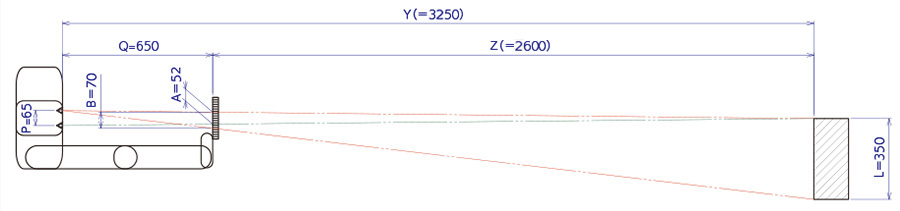
左目で対象物の両端を見てスケールの目盛りを読み、その差をAとします。

右目で対象物の片側端を見てスケールの目盛りを読み、左右の視差寸法をBとします。
このAとBの比がスケールから対象物までの寸法に比例します。

スケールから対象物までの距離Zは

Z＝(A/B)×L×(Q/P)
  ＝(52/70)×350×(650/65)
  ＝2600

となります。

Fig.3

遠方でも簡単に認識できる目標物として乗用車（約４ｍ）、両開きの窓や扉（約1.8ｍ）などがあります。

そして腕を伸ばした位置を基準としたZ寸法で考えると非常に簡単な計算で距離が求まります。条件として両眼のピッチと腕のリーチの比を1:10として固定すると

Z＝(A/B)×L×10

という簡単な式になります。またA、Bは

A＝P×Z/Y

B＝L×Q/Y

となります。例としてL＝4000ｍｍで10ｍごとに計算してみると

以下となり、Z寸法がL寸法を10倍にし、A/Bを乗じた値になります。

Fig.4
対象物の寸法がわかっている場合は両眼視差を使わなくても簡単に距離を求めることが出来ます。
対象物の両端を見てスケールの目盛りを読み、その差をAとします。
対象物までの距離Yは

Y＝(Q×T)/A
  ＝(650×1750)/138
  ≒8243

Fig.4

色々な測定器が発達して便利になっていますが、自分の身体と普段カバンの中に常備しているもので出来ることを知っておくと意外な時に役立ちます。

博士「どうじゃ、あるる。このように自分の身体を使って、いろんなものを測ることができるのじゃ」

あるる「はいっ！　すごいです！　楽しいです！　帰ったらさっそく、おじいちゃんに教えます！」

博士「あるるのおじいちゃんなら、既に知っていると思うがのぅ」

あるる「あああああっ！！！」

博士「ど、どうしたのじゃ?!」

あるる「歩いて測ろうとしたら・・・自然に飛んじゃいました。羽があることを忘れていました・・・」

博士「おお、そうじゃった。あるるは歩くより飛ぶ方が得意じゃったな。ふぉっふぉっふぉ〜（笑）」

あるる「もう、笑い事じゃありませんよ。結構ショックなんですから」

博士「まぁ、そうしょげるな。もっとオトナになったらできるようになるから」

あるる「・・・そういうものですか・・・？」

博士「ああ、そういうものじゃ」