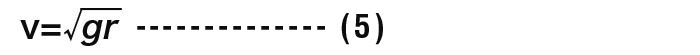みなさん、こんにちは。基礎用語、案内役のあるるです。
今回注目する基礎用語は、コチラ！
↓↓↓
今月の基礎用語：シ　＃047
人工衛星（じんこうえいせい）
（artificial satellite ／human-made satellite）

あるる「博士、博士ぇ〜、聞いてください！」

博士「どうしたのじゃ、あるる。朝から賑やかじゃのう」

あるる「昨日、おじいちゃんに海釣りに連れて行ってもらったんですが、おじいちゃんのスマホ、すごいんですよ〜〜〜っ」

博士「ほう、どうしたんじゃ？」

あるる「お船に乗って海の上にいるのに、おじいちゃんのスマホだけバリバリにつながるんですよ！　他の人は全然つながらないのに、一人だけ、音もクリアで超快適！　すごくないですか？」

博士「人工衛星を使って通信したんじゃな。さすがあるるのおじいちゃん、最先端を行っておるのぅ」

あるる「え〜〜、もうそんなことができる時代なんですか！（驚）」

博士「技術は着実に進歩しておる。今は一部の通信会社が個人向けサービスを提供しておるが、来年にはもっと広がる見通しじゃ」

あるる「やったー、すご〜い、楽しみ〜。人工衛星がんばれ〜〜＼(^o^)／」

博士「ところで、なぜ人工衛星は決まった軌道を回り続けることができるのか、覚えておるかな？」

あるる「あっ・・・以前やりましたよね。確か数字がいっぱい出てきて・・・」

博士「ニヤッ。大切なのは『何速度』だったかの？」

あるる「えっと、えっと・・・・・通信速度！！」

博士「ぶぶー。残念。よし、これからきっちり復習じゃ！」

人工衛星について考えよう

日本の宇宙開発も官民ともに進んでいますが、宇宙関係でもアルファフレームが使用されており、多方面で利用していただいている事に感謝して、今回は人工衛星について力学的側面から考えてみたいと思います。

人工衛星は、なぜ決まった軌道を回り続けることが出来るのでしょうか？

それを理解するために、次のことを考えていきましょう。

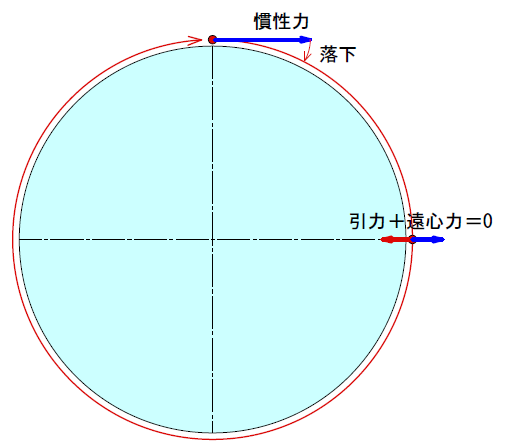
まず、地表すれすれで大砲を打ったとします。その砲弾は、ある距離で地上に落下しますね。引力があるからです。

ところが、砲弾の速度を上げていくと、やがて落下の曲率と地球の曲率が同じになります。

つまり、万有引力で落ちようとしたら、そこに地面が無い状態が続くと考えてください。

地面がない状態に加え、空気が無い状態を仮定すると、砲弾は空気抵抗が無いので速度を保ち、落下せずに1周回って、さらに回り続けます。

この速度を“第一宇宙速度”と言います。

砲弾においては、万有引力によって軌道を曲げられるので、慣性力により外向きの加速度が発生し、いわゆる遠心力を感じることになります。

それは、向心力である万有引力と同じ大きさで向きが逆になるため、この系においては無重力に感じることになります。

「感じる」というのは、実際には重力はあるけれども、回転運動による慣性力（遠心力）と釣り合って感じなくなるという事です。

では、第一宇宙速度を算出してみましょう。

運動方程式 F＝m a より、等速円運動の加速度は v2/r なので

F=m v2/r-------------(1)

=m r ω2------------(2)

Fは、万有引力に等しく

F=G M m/r2-----------(3)

(1)(3)より

G M m/r2=m v2/r------(4)

地表面においては、万有引力＝m g とみなせるので

式(4)は

m g=m v2/r

となり、これをvで解くと

式（5）に各値を代入し

第一宇宙速度は、
秒速約7.9km、時速だと約28,000km にもなります。

なんと新幹線の100倍、ジェット旅客機の30倍以上の速度です。

なお、等速円運動している系から見た時に向心力（引力）の反力として生じている力を遠心力と言います。

向心力（＝遠心力）は速度の2乗に比例しているので、単純計算では新幹線が地球の円周に沿って285km/hで走行した場合には、向心力の10⁻⁴の遠心力が働くことになり、重力が1/10000小さくなります。

理論的に、体重70kgの人は7g軽くなります。

しかし、実際には地球の自転による速度の方が速く（赤道上で1667km/h、東京で1348km/h）、自転と逆方向に移動した場合、合成速度は遅くなるため逆に重くなります。

補足しておくと、緯度によって自転の周速が異なり、緯度が低いほど物体にかかる遠心力は大きいため重力加速度は小さくなるので、同じ質量でも低緯度ほど重量が小さくなります。

式(2)から算出すると、北極点と赤道上では重量差が約0.34％となります。

引力＝質量×重力加速度

重量＝引力－遠心力

さて、次に本題の人工衛星です。

人工衛星は色々な高度で飛んでおり、国際宇宙ステーションは高度400km程度、静止衛星は高度約36000kmと、かなり広範囲で、高度が高いほど速度が遅くなります。

それは重力が半径の2乗に反比例するからで、半径が2倍になれば重力は1/4となります。

円運動の慣性力は、半径に反比例し速度の2乗に比例するので、半径が2倍になれば速度は √1/2 でバランスが取れるわけです。

今回は「ひまわり」などの静止衛星を考えてみましょう。

静止衛星というのは地球との位置関係が変わらないように動いている人工衛星です。これは赤道上の特定高度でしか存在できません。

赤道以外の緯度では重力が地球の中心を向いているため、慣性力とのバランスで斜めの軌道となり、北半球と南半球を行ったり来たりするのです。

静止衛星の高度は35,786kmとなっていますが、面白いので理論計算してみましょう。

ここでは複雑な要素は考えず、単純な2点間の力学として考えます。

前出の式(2)(3)から

G M m/r2=m r ω2

これをrで解くと

r=(G M/ω2)1/3------------(6)

ここで、地球と相対位置が変わらないという事は、角速度が同じという事。

1日かけて1周するわけですが、正確な地球の自転周期は23.9344時間です（太陽の周りを公転しているので24時間より1/365少ない）。

これを式(6)に代入し

ここから地球の半径を引き算して

ｈ（高度）＝42,163ー6,378＝35,785（km）

となり、かなり正確に出ました。

僅かな誤差は地球の質量か半径でしょう。

そして、周速は23.9344時間で半径42.163kmの円を1周するわけなので

42163×2π/23.9344＝11,069 km/h

となります。

また、実際には、地球の重力のばらつき、太陽や月の引力の影響などでのずれを補正するためのガスジェットによる軌道修正が行われているようです。

ところで、卓上の地球儀相当として5千万分の１スケールで考えた場合、その地球儀の直径は255ｍｍとなります。

そして、以下それぞれの地表からの距離を換算してみると

富士山の高さ ----------------------- 0.076 ｍｍ

国際線航空機の飛行高度 ------------ 0.2 ｍｍ

宇宙（定義は高度100km以上）----- 2.0 ｍｍ

国際宇宙ステーションISS ---------- 8.0 ｍｍ

静止衛星の高度 --------------------- 720 ｍｍ

月までの距離 ----------------------- 7.7 ｍ

太陽までの距離 --------------------- 3,000 ｍ

となります。

毎日ニュースの天気予報で見る気象衛星の画像は、赤道上のとても遠いところで撮影されているのです。

なお、電磁波の速度は毎秒30万ｋｍなので、静止衛星と地上との通信時間は片道約0.12秒となります。

人工衛星は、通信、放送、測位、観測など行えますが、今後ますますその用途は拡大して我々の日常生活を便利にしてくれるでしょう。

あるる「ありがとうございます！　大事なのは『宇宙速度」でした。しっかり思い出しました」

博士「よし、宇宙速度は宇宙を語る基本中の基本じゃ。しかと覚えておくように」

あるる「はいっ！！　あと、高度の計算、面白いですねー。もっとやってみたいです」

博士「そうか、それはよかった。その探究心が大切にじゃ」

あるる「はいっ！！！」

博士「ちなみに、おじいちゃんのスマホがつながったのは、代表的な通信衛星であるスターリンク社の衛星じゃ。軌道は550Km、国際宇宙ステーションのやや上じゃな」

あるる「えっと、5千分の1で考えるから・・・11mmですね！」

博士「正解！　ちゃんと理解したではないか。えらいぞ、あるる」

あるる「えへへ、それほどでも♪」

博士「夏は衛星観測にはベストな季節といわれておる。もしかしたら見られるかもしれんのぅ」

あるる「本当ですか？　調べてみます！　みてみたいです！ロマンですねぇ、、これぞ宇宙のロマンです」

博士心の声（今回は『マロンが食べたい』とは言わんのじゃな・・・ちょっと物足りないのぅ）