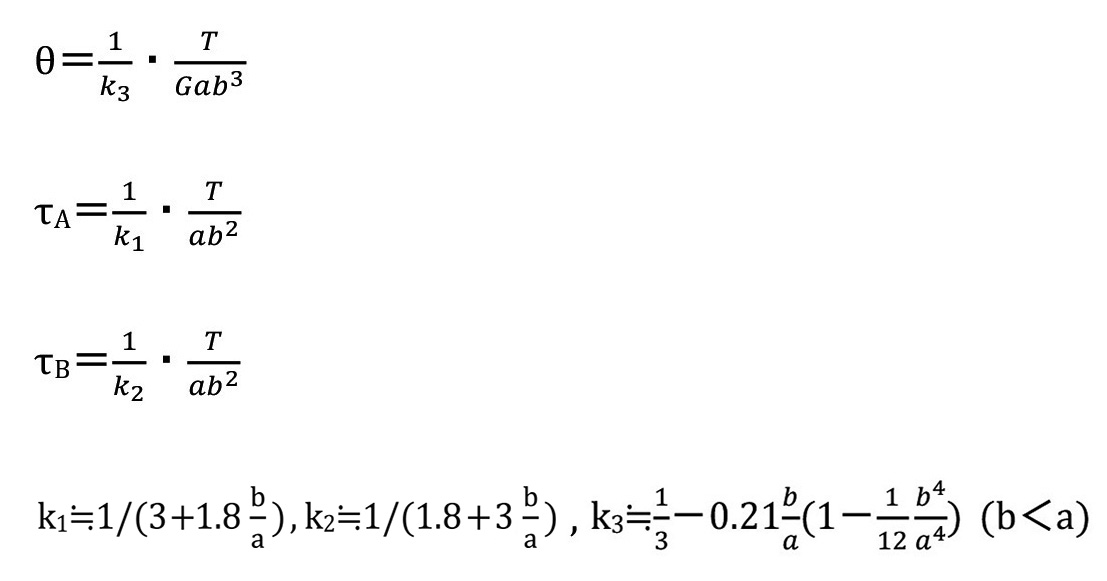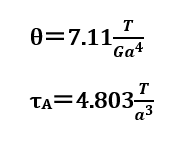【今月のまめ知識 第90回】矩形断面のねじり
公開日時:2020/09/30
とあるのんきな朝のひととき
あるる「ふー、今日も朝からいい汗をかいたなー」
博士「おはよう、あるる。ラジオ体操、まだ続けておるのか? 偉いのう」
あるる「あ、博士、おはようございます。例の「ねじりの体操」もだいぶ上手になりましたよ。ホラ!(えいえい)」
博士「おお、本当じゃ。よくねじれておるぞ。やはり継続は力なりじゃ。スゴイぞ、あるる」
あるる「はい!」
博士「頑張ってるあるるにご褒美じゃ。ほれ!」
あるる「わー、ねじり揚げパンだ\(^o^)/ 美味しそー」
博士「さっきパン屋の前を通りかかったら、実にいい匂いがしてのぅ〜」
あるる「ありがとうございます!! 大好きなんです!!」
博士「まだ熱々じゃ。一緒に食べよう」
あるる「わーい、わーい、うーん、美味しいぃ〜っ!!!」
博士「ふぉっふぉっふぉっ。いい食べっぷりじゃ。もう一個食べてもよいぞ」
あるる「えーーー、いいんですかーーー♪ 食べまーす(もぐもぐ)」
博士「(ニヤッ)そ・の・か・わ・り・・・」
あるる「はっ、そ、その黒い笑いは・・・?!」
博士「今日も【ねじり】について、たっぷり語るぞ。楽しみにしておれ」
あるる「ねじりについて、まだ語ることがあるとは・・・。でも、ま、美味しいからいっか♪(もぐもぐ)」
矩形断面のねじり
矩形断面など、円形断面以外のねじりは弾性学となります。
円形断面では軸線に垂直な棒の横断面は変形を起こした後でも平面を保っており、変形前の半径の線は変形後も直線です。
つまり、薄い円盤が重なっていて、その両端面にねじりモーメントを掛けると、1枚ごとに同じ角度ずつズレを生じて、その薄い円盤は変形しない状態です。
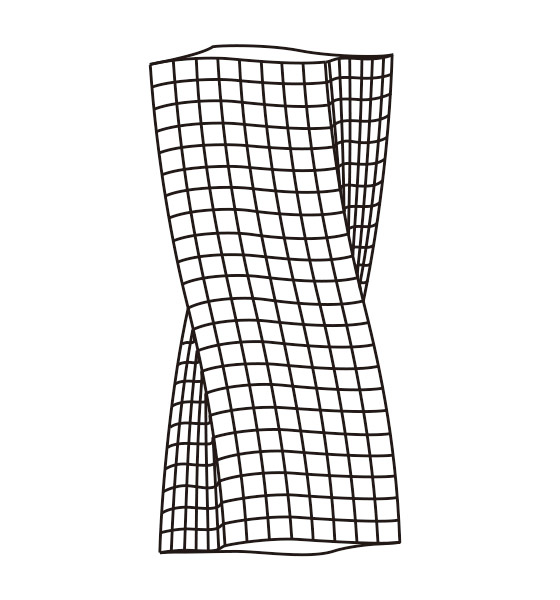
しかし、矩形においてはそうはならず、イメージで言うと、ゴムの丸棒をねじると外周で応力が最大になりますが、矩形断面のゴムの角柱をねじると、Fig.1のように広い面の中央部(中心から一番近いところ)が最も湾曲することが想像できるかと思います。
ここで応力が最大となるわけです。
Fig.1
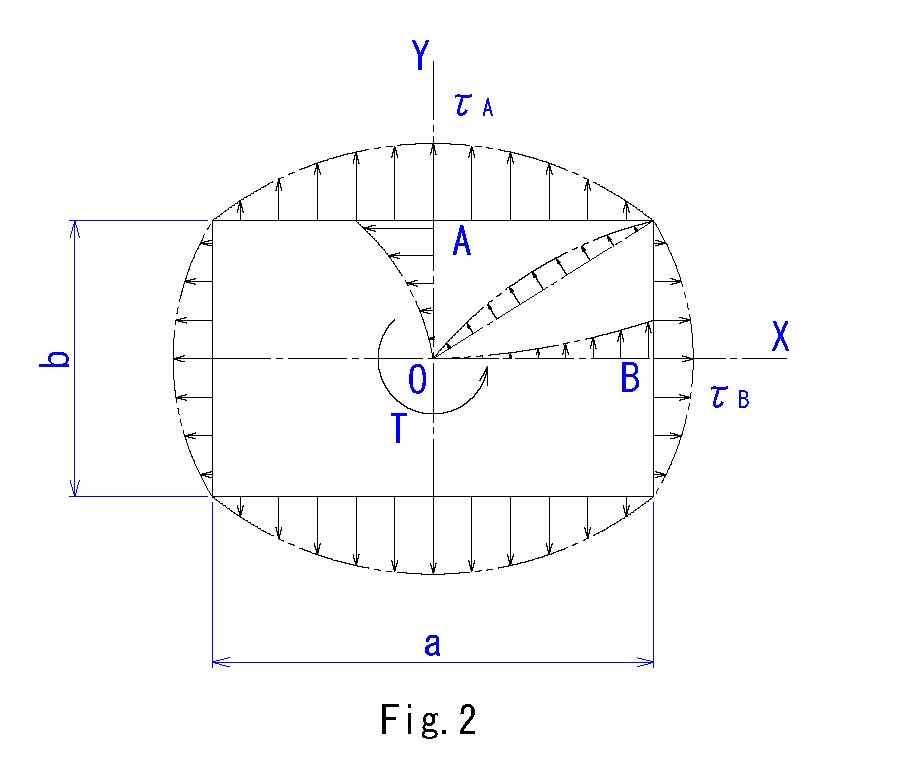
せん断応力は中心Oからの距離に比例しないで、OA,OB上ではFig.2のように分布し、周囲に生ずるせん断応力は辺の中央で最大になり4隅の角では、0となります。
そして、長辺の中央部(中心から最も近い位置)で応力が最大となります。
それらの関係は、近似的に以下のようになります。
θ:単位長さ当りねじれ角
τA,τB:せん断応力
さらに、開断面形状(H鋼やナット溝のあるアルミフレーム)ではまた異なった挙動となります。
Hやコ型においては別に計算式がありますが、ナット溝付きのアルミフレームのような複雑形状では、FEM解析で求めるか、実験するしかありません。
円形断面では断面二次極モーメント( Ip )がありましたが、矩形断面の場合には、サンブナンのねじり定数( J )で表します。
円形断面の場合には先に述べた通り軸線に垂直な横断面は変形しないので両端面も変形後も平面です。
しかし、矩形断面においてはFig.1のイメージ図で見てわかる通り、変形前に対してその横断面は湾曲し、その両端面が完全に拘束されていた場合には軸方向に圧縮力、引張力が掛かり、さらに複雑な問題になります。
その点が円形断面とは異なるので、円形断面以外ではIpに相当する値を、両端の拘束が無いとした場合にサンブナンのねじり定数( J )とします。
アルファフレームの主要なものについてはJの値を準備してありますので必要であればお問い合わせください。
2021年9月9日 k1、k2の近似値算出式を修正しました。
博士「どうした、あるる。やけに大人しいが・・・」
あるる「・・・」
博士「お腹でも空いたか?」
あるる「あ、博士! できました! じゃーん、タオルdeねじりぱ〜ん\(^o^)/」
博士「おお、よくねじれておる・・・じゃない! これ、授業中にこんなものを作っておったのか!」
あるる「いやぁ〜、ねじりの世界の奥深さをしみじみ思っていたら、手が勝手に動いてしまって」
博士「ふぉっふぉっふぉ。その気持ち、わからんではないぞ」
あるる「博士もいろんなモノ、ねじったんですか?」
博士「子供の頃はのぅ、手当たり次第じゃ(笑) 昔から“体験に勝るものはなし”というじゃろう。タオルをねじるのと、ゴムの丸棒をねじるのとでは全くということを、今のうちから肌で覚えるのは良いことじゃ。いろいろ捻ってみると良いぞ」
あるる「はいっ!! 早速やってみます!(キラン)」
博士「くれぐれも、人様の迷惑にならない範囲でやるんじゃぞ」