【今月のまめ知識 第33回】 構造物の転倒に関して
公開日時:2015/12/14
小春日和の昼下がり、突然の「揺れ」があるるたちを襲うーーー
グラグラッ!!!
あるる「わぁっ! 地震だっ!」
あるる「うわぁ〜ん、博士ぇ〜、怖いよぅ〜」
本棚につかまりながら、うずくまるあるる
いつも自信満々なくせに(特にごはん時)、地震にはめっぽう弱いらしい。
博士「そんなところにいたら危ないから、こっちへおいで!」
博士「本棚が倒れたら、下敷きになっちゃうぞ!」
あるる「あ、博士ぇ〜、来てくれたんですねっ!!うわぁ〜ん!(泣)」
博士「よしよし。いい子だ」
−−−ホンの数秒後−−−
博士「ほら、もう治まった」
あるる「(ほっ)よかったぁ〜。本棚も無事でしたね。一冊も落ちてないし…」
博士「まぁ、今回はそんなに強い地震ではなかったからのぅ」
博士「でも、あるるよ。覚えているか? お前は本棚に本を入れすぎて
ばきっと壊しそうになったじゃろう?」
あるる「・・・あ、はい・・・。荷重を知らないときですよね」
博士「しかもあのとき、結構上の段に重たい本を無造作に入れておいたじゃろう?」
あるる「そうでしたっけ?」
博士「もし、あの状態のままだったら、今の地震で本棚は倒れてしまったかもしれんのぅ」
あるる「えっ!! そうなんですか?」
博士「ああ、今頃あるるは本棚の下敷きになって、ペッシャンコだったかもしれん」
あるる「そんなぁっ! 嫌ですよぉ〜、ど根性ガエルのピョン吉みたいには
なりたくないですよぅ〜 (((; ゚ー゚))) ぶるぶる」
博士「ふぉっふぉっふぉっ(笑)
よし、では今日は、“なぜモノが倒れるか”を考えてみようじゃないか、のぅ、ある吉!」
あるる「よしてくださいって!」

構造物の転倒に関して
機械設備から棚まで、あらゆる構造物において地震などによる転倒のリスクがあります。
床面で滑れば転倒はしませんが、その場合、衝突の危険があります。
今回は滑りが無いとしたときの転倒を考えます。
例えば、地震等で水平方向に加速度がかかったとして、
それを静荷重に置き換えて力関係を考えてみます。
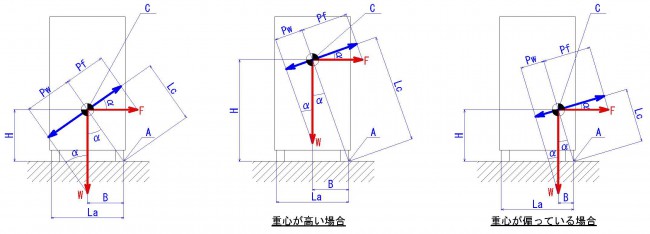
上図は、左から右方向に力がかかった場合を表しています。
この場合、点Aを支点として回転しようとします。
地震により作用する力は、
点Aに対して時計回りのモーメントに、
本体の自重は反時計回りのモーメントとなり、
どちらが大きいかで、転倒するかどうかが決まります。
Wは自重であり、重心点Cから鉛直方向に作用します。
Fは地震の揺れにより横に押される力で、
質量に加速度を乗じた値が重心点Cから水平方向に作用します。
加速度については、【今月のまめ知識 第7回】 耐震強度についてでお話しましたが、
重力加速度は約980cm/sec2ですから980galになります。
仮に揺れの加速度を600galとすると、重力加速度は980galなので、質量mに対し
W=980・m
F=600・m
となり、この場合FはWの約61%程度と言うことになります。
次に角αを求めます。
α=tan-1(B/H)
揺れによる力Fの点Aから見た接線方向の分力Pfは
Pf=F・cosα
揺れによる点A回りのモーメントMfは時計回りで
Mf=Pf×Lc
自重による力Wの点Aから見た接線方向の分力Pwは
Pw=W・sinα
自重による点A回りのモーメントMwは反時計回りで
Mw=Pw×Lc
ここで
Mf>Mw ならば転倒する
Mf<Mw ならば転倒しない
ということになります。
重心が高い場合や、偏っている場合には、角αが小さくなり、
Pwに対してPfが大きくなるので転倒のリスクが高まります。
これらの関係については計算をしなくても、上図のように作図で求める事が出来ます。
実際の地震においては周期を持った繰り返しの荷重がかかり、
また上下方向の揺れも加わり複雑なものとなりますが、
このように単純におおよその見当を付けることは出来ます。
また、アンカーボルトを施工した場合には、その抜け強度を加味します。
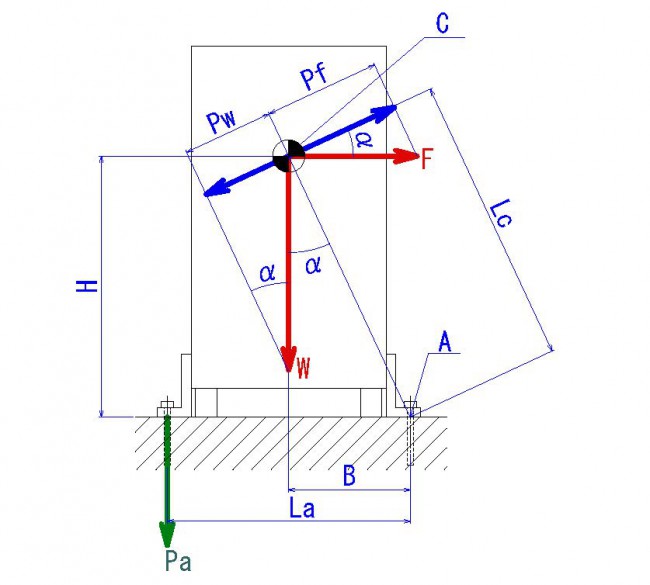
この場合は上記に加え、アンカーの強度が反時計回りのモーメントに加わります。
アンカーの強度をPaとした場合に点A回りのモーメントMaは
Ma=Pa×La
となり
Mf>Mw+Ma ならば転倒する
Mf<Mw+Ma ならば転倒しない
ということになります。
重心とは
物体には、その物体がどのような姿勢状態にあっても必ずつりあいを保つ点があります。
この点で物体を支えると、どのような姿勢状態でもその物体は安定して静止状態を
保つことができ、このような点を重心といいます。
重心は座標の原点を決め、その原点を中心としたモーメントの総和として求めます。
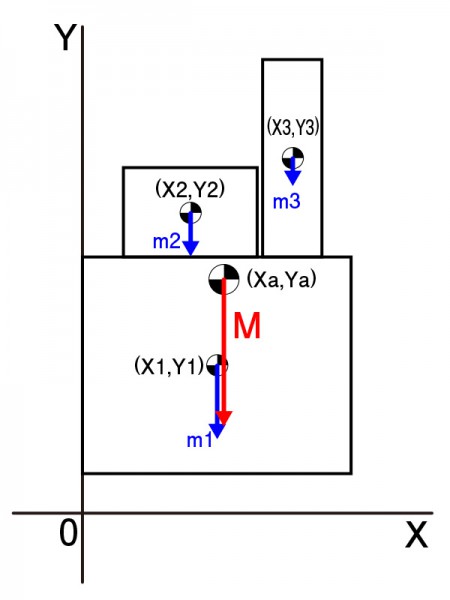
全体の質量をM、全体の重心座標を(Xa,Ya)とし、
各要素部の質量をmn、その重心点座標を(Xn,Yn)とすると
Xa=(m1X1+m2X2+・・・・・+mnXn)/M
Ya=(m1Y1+m2Y2+・・・・・+mnYn)/M
M=m1+m2+・・・・・+mn
となります。
博士「・・・ということじゃ。わかったかの?あるる」
あるる「う、あ、はい・・・公式は覚えきれませんでしたが、重心が大事!ということは、よくわかりました!」
あるる「しかも、重心は低い位置で、“つりあい”が大事なんですよね♪」
博士「まぁ、今日の理解は、その辺でよいじゃろう。公式はゆっくり覚えていけばよいぞ」
あるる「それにしても、博士はどっちなんでしょうね?
博士「なにがじゃ?」
あるる「重心ですよ、じゅ・う・し・ん。足は短いから重心は下とも言えるし、でも、頭が大きいから重心は上かも・・・」
博士「こりゃ、あるる、言いにくい事をスバズバ言いおって! 師に対してそんなことを言うもんじゃないぞ!」
あるる「わーい、ごめんなさーーい \(>o<)/」
博士「これでもバランスはしっかり取れているんじゃ。なんといってもわしは、腹が据わっているからのぅ。
ふぉっふぉっふぉっ」

果たして博士の重心は?