いまさら聞けない基礎用語!【キ】#022 帰納法
公開日時:2023/06/28
昨日?今日?明日? 帰納法ってなんだっけ?
みなさん、こんにちは。基礎用語、案内役のあるるです。
今月注目する基礎用語はコチラ!!
↓↓↓
今月の基礎用語:キ #022
帰納法(きのうほう)
induction
(inductive method/Inductive Approach)
「帰納法」が出てきたのは、ちょうど豆知識100回目となった
【今月のまめ知識 第100回】直交座標から方法序説、そして演繹法と帰納法
でした。哲学者のデカルトのお話です(覚えてますか?)
「哲学」と聞いちゃうと難しいイメージですが、とっても興味深い内容ですので、あるると一緒に復習していきましょう\(^o^)/
博士「おーい、あるるよ〜。なぞなぞを出すぞ〜」
あるる「なんですか、急に。いいですよ、どうぞ」
博士「昨日と今日にあって、明日にはないもの、な〜んだ?」
あるる「えっと・・・きのう、きょう、あした・・・。えっとえっと・・・」
博士「(ニヤニヤ)」
あるる「あっ!わかったっ! 「き」と「う」だ!!」
博士「正解。やるな、あるる。では、次の問題じゃ。
今日や明日より、昨日勉強しておけばよかったっと思うものって、な〜んだ?」
あるる「へ? 昨日? 勉強?・・・ えーーなんだろう?」
博士「ヒントじゃ。さっきの答えは、なんじゃったかの?」
あるる「え? さっきは「き」と「う」ですけど・・・。
きとう、きとう・・・あっ! きのうほう(帰納法)?」
博士「正解じゃ\(^o^)/ そろそろ帰納法の復習でもどうかと思っての」
あるる「もう、博士ったら、だったらストレートに言えばいいじゃないですか。なぜなぞなぞ?」
博士「最近のマイブームじゃ。なかなかよかったじゃろ?」
あるる「博士の好み、いまいち謎です・・・」
方法序説、そして演繹法と帰納法と直交座標
現代において誰もが知っている直交座標の元を作ったと言われている17世紀フランスの哲学者・数学者であるルネ・デカルト。
歴史上で数多くの偉大な数学者がいますが、数学を普遍的なものにしてすべての事を数学的に考えようとし、真理の探究方法として「方法序説」を執筆しました。
その中で「演繹法」に至ったデカルトと、その対極にある「帰納法」について結び付けてみました。
デカルトの方法序説
デカルトは「わたしは何よりも数学が好きだった。論拠の確実性と明証性のゆえである」と言っています。
しかし、機械を作るためだけではなく、数学はもっといろいろなことに役立つと考え、その考え方をわかりやすく普遍的なものにしたいと思ったのです。
そうしてデカルトは、1637年に「方法序説」を世に出しました。
正式な題名は「理性を正しく導き、諸学問において真理を探求するための方法についての序説、付、この方法の試論たる屈折光学、気象学、幾何学」でした。
その序説において、物事を考える手法はシンプルであるのが良いとして、以下の四つの規則を示しました。
1) 明証性---本当に当たり前なのかを熟考する
2) 分析------検討する難問を細かく分解する
3) 総合------順序立てて認識を深める
4) 枚挙------全体を復習する
これを流れで言うと、以下のようになります。
当たり前だと思っていることを、改めて「本当にそうなのか?」と疑う
↓
課題を細かく分け、考えやすくする
↓
答えを出すにあたり、順序が無くてもあえて順序を付け、数学の証明のように導いていく
↓
最後に全体を振り返り、漏れがないことを確認する
という事です。
ちなみに、デカルトは第一の明証性の規則を突き詰めてすべてを疑った結果、残ったのは「それを考えている(疑っている)自分の理性だけだ」として「我思う、故に我あり」と言ったわけです。
17世紀の欧州において、科学も医療も占星術も、学問はすべて一緒くたでした。
今では学校でも色んな科があり、病院でもたくさんの科に分かれています。
これは難問を解くために、細かく分けて考えると言うことの結果です。
演繹法と帰納法
デカルトの思考法は演繹(えんえき)法であり、近代合理主義の出発点となりました。
演繹法は、疑いようのない普遍的原理から論理的推論によって個別の事柄を導く方法です。
これに対する帰納法は、実験・実証による経験主義に基づく推論です。
演繹法では、前提が正しい場合、正しい結論が導きださされますが、三段論法がそうであるように、前提が間違っていると誤った結論となります。そこが演繹法の弱点です。
一方、帰納法では、前提が正しいからといって結論が正しいとは限りません。経験をあらゆる知識の源泉と見なします。
帰納法を提唱したのは「知は力なり」と言ったイギリスのフランシス・ベーコンだと言われています。
知識を得るためには、まず先入観や偏見を取り除いて、ありのままに観察する。そして観察や実験に基づく経験で結論を出す、というのが帰納法の基本的な考え方ですが、全事例を網羅しないかぎり、結論からもれる事例が存在する可能性があるというのが、帰納法の弱点でもあります。
この2つの推論方法で面白い話があります。
現在においては、物体の落下速度は時間の経過による関数であることは誰もが知っています。
デカルトは「真空中の石の落下」問題に関して、図形化しながらも、速度と距離と力の関係で図形化したため、速度を距離の関数と誤って考えてしまいました。
しかし、デカルトと親交のあったベークマンは、実験的数値を知っていたため、時間を関数とする正しい答えを導き出しました。
不安定な偶然要素に左右される実験を疑い、数学のみで考えたデカルトと、実験物理学でその結果から数学に入っていくベークマン。正しかったのはベークマンです。
そして少し先行して、イタリアではガリレオ・ガリレイがこの手法(自然現象を数学を利用して研究する)を行っており、この3人が現代の自然科学へと向かうきっかけを作ったというわけです。
デカルトが行った図形化して考えるという事。そして、物体に運動の軌跡を微小部分に分割し、これを再び総合すると言う微積分学の基となる考え方が、ライプニッツ、さらにはニュートンへと引き継がれ、解析幾何学、微積分学が確立されていく過程となったと言えるでしょう。
数学的な筋の通った理屈の積み上げが、科学と合理主義を生んだわけです。
演繹法も帰納法も論理的推論方法ですが、優劣のあるものではなく、目的によって適する方を使い、場合によっては一方の結論を他方で検証することで、より良い結果を導くことが出来るでしょう。
どちらも合理性に基づいていますが、見方によっては「プロダクトアウト/マーケットイン」という対比とも似たものを感じます。
現代において色々な思考法がありますが、やはりそれらは数学が基になっていることを感じます。
前提 → 推論 → 結論
この流れの中で、「□□シンキング」と言われる複数の思考法は互いに補完関係にあり、デカルトとベークマンのように良い意味で競い合える仲間を見つけていきたいものです。
デカルト座標
では、デカルトの功績のひとつである「デカルト座標」を見ていきましょう。
デカルト座標、いわゆる直交座標は平面上に二本の直交する座標軸を引き、それを刻んで数値を当てはめたもので、二つの実数の組によって平面上の点の位置を表す方法です。
座標の考え方はデカルト以前にも存在しており、また現在のような直交軸を基準としたグラフは、デカルトの書物には出てきません。
しかし、幾何学上の図形の問題が代数によって表現できることを初めて示したのがデカルトでした。
幾何学と代数学を統一し、解析幾何学のベースを作ったと言う意味で、直交座標はデカルト座標と呼ばれ、座標の発明者と言われているわけです。
それまでの幾何学はユークリッド幾何学で、形や大きさ、角度などを定義するものであり、代数学は抽象的な文字の世界で、代数記号は各人各様で難解かつ複雑でした。
記号的代数学を創始したヴィエトは、未知数を母音文字(A,E,I,O,V,Y)、既知数を子音文字(B,G,D,…)で表記して、平方はquadratum,planum、立方はcubusなどの語で表記しました。
デカルトは難解な代数学をシンプルで普遍的なものにするため、未知数にx,y,…、既知数にa,b,c,…を用い、
さらに画期的な記号法によって言語の部分を無くしたのです。
それまで、2A cubusと書いていたものを2x³と書き、量の代数学の基を作り上げました。
中学校で習う、未知数の表記や指数の表記はデカルトが決めたものだったのです。
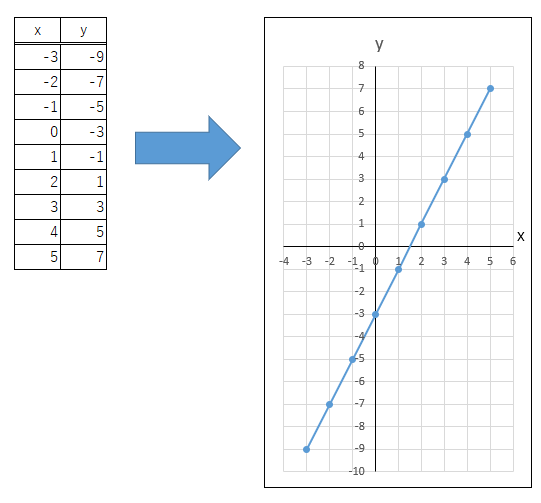
二元一次方程式、y=ax+b において、
a=2、b=-3として独立変数のxに対して従属変数の y を計算してみると
下表の通りとなり、そしてデカルト座標があることで x と y の値を視覚化することが出来ます。
座標により、数や式を図形に出来たわけです。
デカルト座標
おまけ
「方法序説」第六部に、今の私たちが心しておくべき一節が書いてあるので、最後にお伝えしておきます。
「なお、この機会に後世の人たちに、わたし自身が公表したものでなければ、わたしの意見だとほかの人が言っても、けっして信じないようにお願いしたい」
私たちは難解な学問であればあるほど、簡単に、そして手軽に理解しようと、原書は読まずに解説本で済ませる傾向があります。
しかし、物事の真理を知りたければ、他人のフィルターを通して簡略化されたものではなく、まずは本人の言葉を自分の頭で解釈することが大切なのだと、デカルトは私たちに教えてくれているように思います。いかがでしょう?
あるる「いや〜、何度聞いてもデカルトさんは頭良過ぎて、ビックリです」
博士「そうじゃのう。デカルト氏が今の時代を生きていたら、今以上に技術も発展したかもしれん。そう考えると、ロマンじゃのぅ・・・」
あるる「ロマンですね・・・」
博士「あるるはロマンよりマロンじゃろう?」
あるる「わかってますね(笑)あっ! マロンで思い出した!
なぞなぞ博士に出題です」
博士「なぞなぞか? よし、かかってまいれ」
あるる「『栗栗栗栗太』と書いてなんて読む?」
博士「クリクリ? クリしーた? えー、なんじゃろう?・・・」
あるる「ふぉっふぉっふぉっ。答えは『フォークリフト」でした」
博士「なるほど! こりゃやられた! やっぱりなぞなぞも奥が深いのぅ」
あるる「これもロマン、ですね (^_−)−☆」
(出典:大人のなぞなぞ】97問目)
https://www.nazo2.net/app_capture/quiz/otonano_nazonazo/97.html