博士「おはよう、あるる。今日も楽しく学んでいこうな」

あるる「はいっ！　朝からカツ丼食べてきましたんで、スタミナばっちりです！」

博士「それはすごいのぅ　なんて強い胃袋なんじゃ」

あるる「あっ！技術者はいちがいに「強い」って言っちゃいけないんですよ！　
　　強さにもいろいろあるって、『第5回　強さって何？』 で教えくれたの、博士じゃないですか！」

博士「おお、こりゃ〜本取られたのぅ。そうじゃった、そうじゃった。よく覚えていたな、えらいぞ、あるる」

あるる「はいっ！　ネバネバパワーのおかげです！」

博士「よし、その調子じゃ！　粘りといえば弾性じゃ。そうじゃな、あるる」

あるる「その通りですともっ！やっぱり、男たるもの、粘りがなければ！　こう、腰が入って・・・」

博士「そうそう、力士はやっぱり粘り腰じゃ・・・って、その“男性”ではない、“弾性”じゃ！」

あるる「あはは。博士もついに「ノリツッコミ」ができるようになったんですね！　すごーい」

博士「いや、。。。それほどでも。。。（照れ）」

前回、前々回で弾性係数についてお話ししました。

また【今月のまめ知識 第5回】強さって何？　〜引張強さと耐力〜では、

弾性係数はフックの法則における比例係数である事をお話ししていますので、

今回はこの関係をまとめておきます。

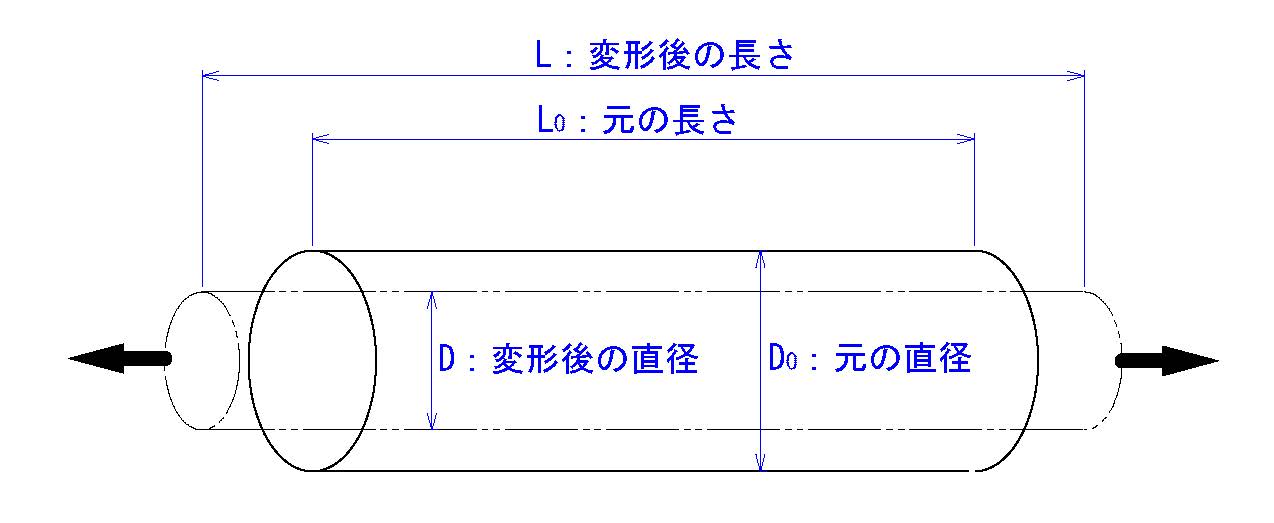
縦弾性係数：E＝σ／ε

横弾性係数：G＝τ／γ

σ：垂直応力

ε：垂直ひずみ

τ：せん断応力

γ：せん断ひずみ

ε＝（L－L₀）/L₀

γ＝（D－D₀）/D₀

例として、1mの棒に70N/mm²の引張り応力が掛かった時、

1mmの伸びが生じた材料の縦弾性係数は

70/0.001＝70,000(N/mm²)

となるわけです。

ここまでは力学的に見た材料の特性値ですが、

実際の梁の剛性はこれに幾何学的要素（断面の形状、寸法）を加える必要があります。

そのための特性値として、以下のものがあります。

A：断面積

I：断面2次モーメント

Ip：断面2次極モーメント

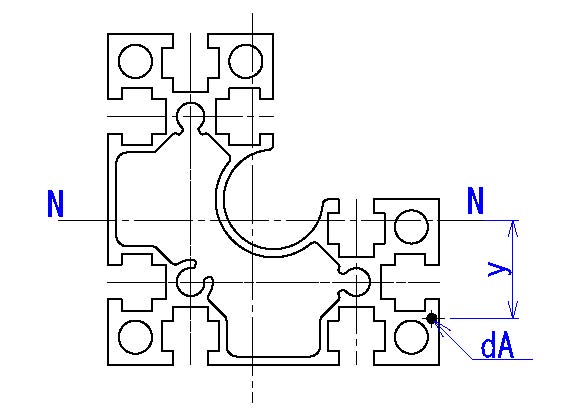
・断面2次モーメント

「曲がる」ということは、ある軸を中心に回転しているということになりますが、

断面を微小断面積dAに分解し、それに回転軸からの距離yの2乗を掛算し、それらを全て合算した値です。

I＝∫(y²dA)

なお、回転軸の交点は図心となります。

・断面2次極モーメント

これはねじりに関するもので、微小断面dAにその同一平面内の1点からの距離rの2乗を掛算し、

それらを全て合算した値です。

Ip＝∫(r²dA)

ただし、構造用アルミフレームのように、外側に凹み形状を持つものではこれが成り立ちません。

当社では別手法により各型番でのIp値を算出しています。

圧縮・引張りには断面積、せん断には断面積、曲げには断面2次モーメント、

ねじれには断面2次極モーメントが係わります。

つまり

A×E→伸び剛性

A×G→せん断剛性

I×E→曲げ剛性

Ip×G→ねじり剛性

となるわけです。

異なった材質、異なった形状のものであっても、これらを比較することで、どちらが剛性が高いか（変形しにくいか）を知ることができます。

博士「どうじゃな、あるるよ。わかったかの？」

あるる「はいっ！　ちょっと式が難しかったですが・・・諦めず勉強してみます！」

博士「えらいっ！偉いぞ、あるる！　勉強も相撲も［粘り］が大切じゃ！　こう、腰をグッといれてな・・・」

あるる「そうそう、腰を入れてですよね・・・って、また同じネタですか！」

博士「えへへ・・だって気に入っちゃったんだも〜ん」

あるる「やれやれ、子供みたいな人ですねぇ〜（ふぅ〜）」